Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

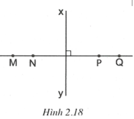
Ta có M N ⊥ x y ; P Q ⊥ x y (vì xy là đường trung trực của NP). Qua điểm N chỉ vẽ được một đường thẳng vuông góc với xy, suy ra ba điểm M, N, P thẳng hàng. (1)
Ta có N P ⊥ x y ; P Q ⊥ x y . Qua điểm P chỉ vẽ được một đường thẳng vuông góc với xy, suy ra ba điểm N, P, Q thẳng hàng. (2)
Từ (1) và (2) suy ra các điểm M, N, P, Q thẳng hàng vì chúng cùng thuộc đường thẳng NP

a) xét tam giác MHN và tam giác MHP có
\(\widehat{MHN}\) = \(\widehat{MHP}\)(= 90 ĐỘ)
MN = MP ( tam giác MNP cân tại M)
MH chung
=> tam giác MHN = tam giác MHP (cạnh huyền cạnh góc vuông)
b) vì tam giác MHN = tam giác MHP (câu a)
=> \(\widehat{M1}\)= \(\widehat{M2}\)(2 góc tương ứng)
=> MH là tia phân giác của \(\widehat{NMP}\)
bạn tự vẽ hình nhé
a.
vì tam giác MNP cân tại M=> MN=MP và \(\widehat{N}\)=\(\widehat{P}\)
Xét tam giác MHN và tam giác MHP
có: MN-MP(CMT)
\(\widehat{N}\)=\(\widehat{P}\)(CMT)
MH là cạnh chung
\(\widehat{MHN}\)=\(\widehat{MHP}\)=\(^{90^0}\)
=> Tam giác MHN= Tam giác MHP(ch-gn)
=> \(\widehat{NMH}\)=\(\widehat{PMH}\)(2 GÓC TƯƠNG ỨNG) (1)
và NH=PH( 2 cạnh tương ứng)
mà H THUỘC NP=> NH=PH=1/2NP (3)
b. Vì H năm giữa N,P
=> MH nằm giữa MN và MP (2)
Từ (1) (2)=> MH là tia phân giác của góc NMP
c. Từ (3)=> NH=PH=1/2.12=6(cm)
Xét tam giác MNH có Góc H=90 độ
=>\(MN^2=NH^2+MH^2\)( ĐL Py-ta-go)
hay \(10^2=6^2+MH^2\)
=>\(MH^2=10^2-6^2\)
\(MH^2=64\)
=>MH=8(cm)

e) Gọi O là giao điểm của IP và HK. Chứng minh \(\widehat{MON}\) = 180o + \(\widehat{PMO}+\widehat{PNO}+\widehat{HIK}\)

Bạn coi thử zùm mình..
Đó là trắc nghiệm đề thi HK1 của mình đó..
Mình chọn câu A sai..Câu đúng phải là câu B..
Mình không hiểu
nếu MN//AB và NP//AB thì
A MN⊥NP
B MN//NP
C M,N,P thẳng hàng
D N nằm giữa M và P