Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

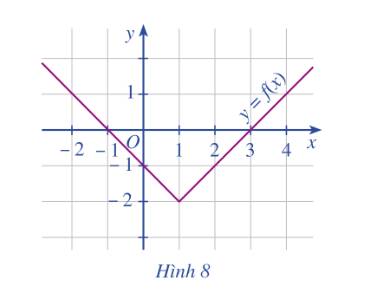
a) Quan sát đồ thị:
điểm \(\left( {1; - 2} \right)\) (tức là có x =1; y=-2) thuộc đồ thị.
điểm \(\left( {2; - 1} \right)\) (tức là có x=2; y=-1) thuộc đồ thị hàm số.
điểm (0;0) không thuộc đồ thị hàm số.
b) Từ điểm trên Ox: \(x = 0\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 0 \right) = - 1\)
Từ điểm trên Ox: \(x = 3\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 3 \right) = 0\)
c) Giao điểm của đồ thị và trục Ox là điểm \(\left( {3;0} \right)\).

a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)

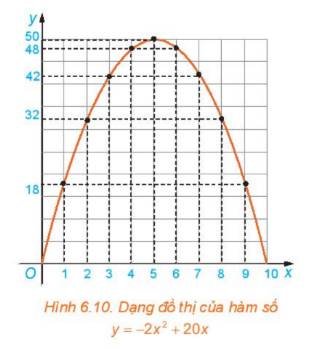
a) Ta có đồ thị hàm số \(y = - 2{x^2}\)
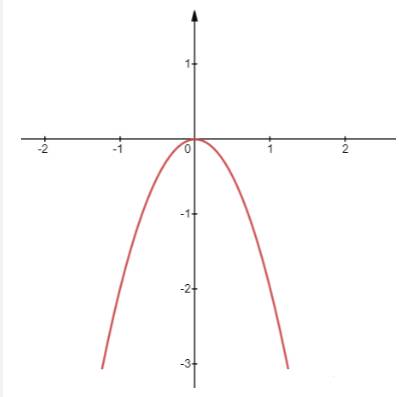
Nhìn vào 2 đồ thị, ta thấy dạng đồ thị của hàm số \(y = - 2{x^2} + 20x\)giống với dạng đồ thị \(y = - 2{x^2}\)
b) Tọa độ điểm cao nhất là \(\left( {5;50} \right)\)
c) Ta có: \(S(x) = y = - 2{x^2} + 20x = - 2({x^2} - 10x) = - 2({x^2} - 2.5.x + 25) + 50 = - 2{(x - 5)^2} + 50\)
\({(x - 5)^2} \ge 0 \Rightarrow - 2{(x - 5)^2} + 50 \le 50 \Rightarrow S(x) \le 50\)
Do đó diện tích lớn nhất của mảnh đất rào chắn là 50 \(({m^2})\) khi x = 5.

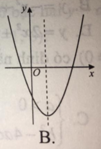
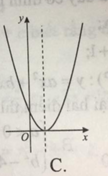
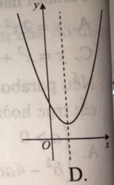
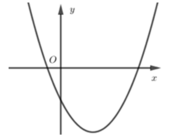
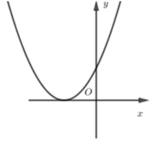
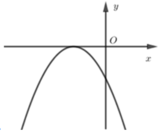
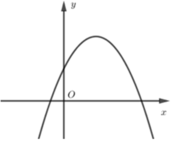

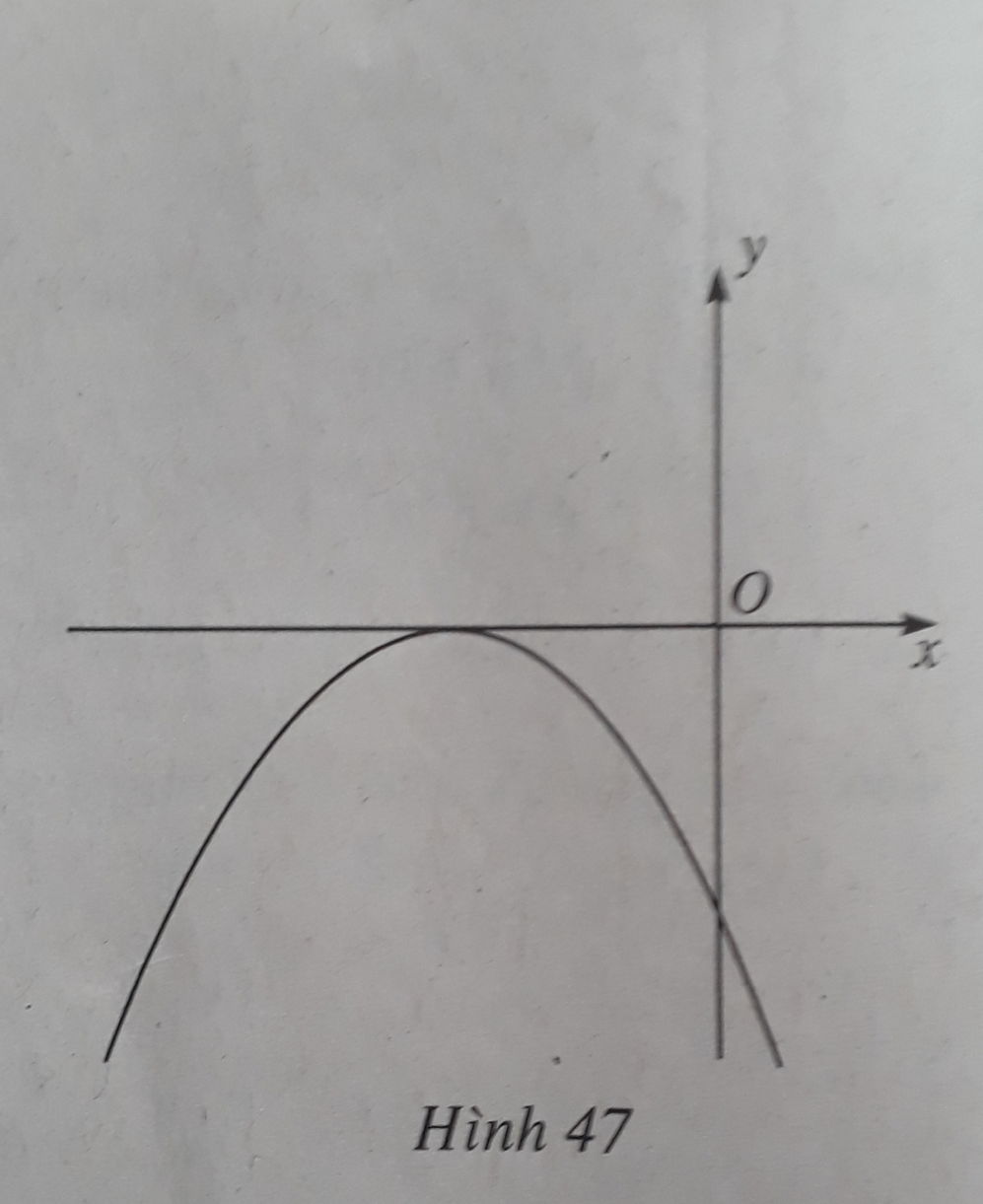

Ta có: x = − b 2 a > 0 nên trục đối xứng nằm bên phải trục Oy
Đồ thị cắt trục tung tại điểm (0; c) nằm dưới trục hoành ( vì c < 0).
Do đó, đồ thị B là đồ thị của hàm số đã cho.
Đáp án B