Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
$BC=\frac{5}{4}AC$
$BC=\frac{5}{3}AB$
$\Rightarrow \frac{5}{4}AC=\frac{5}{3}AB$
$\Rightarrow AC=\frac{5}{3}AB: \frac{5}{4}=\frac{4}{3}AB$
Chu vi tam giác:
$AB+BC+AC=108$
$AB+\frac{5}{3}AB+\frac{4}{3}AB=108$
$AB(1+\frac{5}{3}+\frac{4}{3})=108$
$AB.4=108$
$AB=27$ (cm)
$AC=\frac{4}{3}AB=\frac{4}{3}.27=36$ (cm)
Diện tích tam giác: $AB.AC:2=27.36:2=486$ (cm2)

Tổng độ dài hai cạnh AB và AC:
30 - 13 = 17 (cm)
Tổng số phần bằng nhau:
5 + 12 = 17 (phần)
Cạnh AB dài:
17 . 5 : 17 = 5 (cm)
Cạnh AC dài:
17 . 12 : 17 = 12 (cm)
Diện tích tam giác ABC:
5 . 12 : 2 = 30 (cm²)
Tổng độ dài 2 đáy AB và AC là :
30 - 13 = 17 ( cm )
Tổng số phần bằng nhau là
5 + 12 = 17 ( phần )
Cạnh AB dài là
17 : 17 x 5 = 5 ( cm )
Cạnh AC dài là :
17 - 5 = 12 ( cm )
Diện tích hình tam giác vuông ABC là
12 x 5 : 2 = 30 ( m2)
Đáp số : 30 m2

Lời giải:
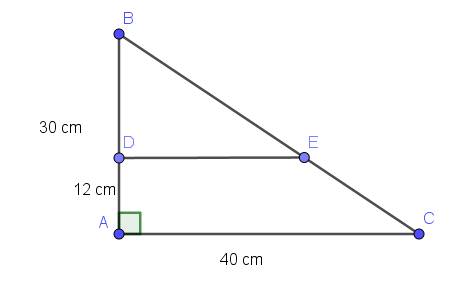
$BD=AB-DA=30-12=18$ (cm)
Diện tích tam giác ABC:
$AB.AC:2=30.40:2=600$ (cm2)
Diện tích tam giác ABC cũng bằng;
$S_{BDE}+S_{ADEC}=BD.DE:2+(DE+AC).AD:2$
$=18.DE:2+(DE+40).12:2$
$=9DE+6(DE+40)$ (cm2)
Vậy: $600=9DE+6(DE+40)=15DE+240$
$\Rightarrow DE=(600-240):15=24$ (cm)
Diện tích hình thang DECA:
$(DE+AC).DA:2=(24+40).12:2=384$ (cm2)

Gọi AH là cc tương ứng với BC
Áp dụng HTL: \(AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\)
Định lí Pitago:Bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh còn lại.
Từ đề bài, ta có 2 cạnh góc vuông là: AB, AC
Cạnh huyền là: BC
Ta có hệ thức từ định lí Pitago: \(BC^2=AB^2+AC^2\)
\(\Rightarrow AB^2=BC^2-AC^2\Rightarrow AB=\sqrt{BC^2-AC^2}\)
\(\Rightarrow AC^2=BC^2-AB^2\Rightarrow AC=\sqrt{BC^2-AB^2}\)
Chúc bạn buổi tối vui vẻ nha ^^