Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi s là quãng đường rơi của giọt nước mưa từ lúc đầu đến điểm cách mặt đất 100 m, t là thời gian rơi trên quãng đường đó, ta có : s = 1/2(g t 2 ) (1)
Mặt khác, quãng đường rơi từ lúc đầu đến mặt đất là s + 100 và thời gian rơi trên quãng đường đó là t + 1 giây.
Ta có : s + 100 = 1/2*g t + 1 2 (2)
Từ hai phương trình (1) và (2) ta rút ra : t = 100/g -0.5 ≈ 9.7(s) ⇒ s = 461(m)
Vậy, độ cao ban đầu của giọt nước mưa lúc bắt đầu rơi là:
s +100 = 561 m.

Mong mọi người giải với hướng dẫn chi tiết hộ em với ạ . Em làm nhiều lần nhưng vẫn ko ra được đáp án ạ :((((Em cảm ơn !!!
C1: Tóm tắt:
g=10m/s2
s(1s cuối)=2s(1s trước)
s=h(vật được thả)=?m
Giải
Quãng đường tổng cộng vật đi được khi thả ở độ cao ban đầu là:
s1=\(\frac{1}{2}gt^2\)=\(\frac{1}{2}.10.t^2\)=5t2(m)
Quãng đường vật rơi trước một giây cuối là:
s2=\(\frac{1}{2}gt^2\)=\(\frac{1}{2}.10.\left(t-1\right)^2\)=5\(.\left(t-1^{ }\right)^2\)(m)
Quãng đường vật rơi trong một giây cuối cùng là:
\(s_3=s_1-s_2=5t^2-5.\left(t-1\right)^2\left(m\right)\)
Quãng đường vật rơi trước hai giây cuối là:
\(s_4\)=\(\frac{1}{2}gt^2=\frac{1}{2}.10.\left(t-2\right)^2=5\left(t-2\right)^2\left(m\right)\)
Quãng đường vật rơi được trong một giây trước một giây cuối cùng là:
\(s_5=s_2-s_4=5\left(t-1\right)^2-5\left(t-2\right)^2\left(m\right)\)
Theo đề bài cho quãng đường vật rơi trong 1s cuối cùng gấp đôi trong 1s trước đó nên:
s3=2s5↔\(5t^2-5\left(t-1\right)^2=2\left[5\left(t-1\right)^2-5\left(t-2\right)^2\right]\)→t=2,5(s)
Vậy quãng đường tổng cộng vật đi được khi thả ở độ cao ban đầu(vật được thả ở độ cao) là:
s=h=\(\frac{1}{2}gt^2=\frac{1}{2}.10.2,5^2=31,25\left(m\right)\)

độ cao h là
\(h=\dfrac{1}{2}gt^2=\dfrac{1}{2}\cdot10\cdot3^2=45\left(m\right)\)
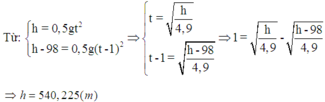


Gọi s là quãng đường rơi của giọt nước mưa từ lúc đầu đến điểm cách mặt đất 100 m, t là thời gian rơi trên quãng đường đó, ta có : s = 1/2(gt2t2) (1)
Mặt khác, quãng đường rơi từ lúc đầu đến mặt đất là s + 100 và thời gian rơi trên quãng đường đó là t + 1 giây.
Ta có : s + 100 = 1/2*g(t+1)2t+12 (2)
Từ hai phương trình (1) và (2) ta rút ra : t = 100/g -0.5 ≈ 9.7(s) ⇒ s = 461(m)
Vậy, độ cao ban đầu của giọt nước mưa lúc bắt đầu rơi là:
s +100 = 561 m.
Tham khảo đâu??