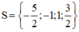AB
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
26 tháng 10 2018
Đáp án A
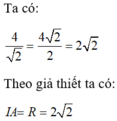
Do đó, điểm A nằm trên đường tròn đã cho. Khi đó, qua điểm A ta vẽ được đúng 1 tiếp tuyến đến đường tròn (I).
P
1
20 tháng 10 2019
\(Cos_{\widehat{E}}=\frac{25}{EF}\Rightarrow Cos_{42^0}=\frac{25}{EF}\Rightarrow EF=\frac{25}{Cos_{42^o}}=33.64\)
LM
0
KT
4 tháng 7 2018
a) \(\sqrt{9-4\sqrt{5}}-\sqrt{9+4\sqrt{5}}=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{\left(\sqrt{5}+2\right)^2}\)
\(=\left(\sqrt{5}-2\right)-\left(\sqrt{5}+2\right)=-4\)
b) \(\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}=\frac{1}{\sqrt{2}}.\left(\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\right)\)
\(=\frac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(\sqrt{7}+1\right)^2}\right)\)
\(=\frac{1}{\sqrt{2}}\left(\sqrt{7}-1-\sqrt{7}-1\right)=-\sqrt{2}\)
c) \(\sqrt{94-42\sqrt{5}}-\sqrt{94+42\sqrt{5}}=\sqrt{\left(7-3\sqrt{5}\right)^2}-\sqrt{\left(7+3\sqrt{5}\right)^2}\)
\(=7-3\sqrt{5}-\left(7+3\sqrt{5}\right)=-6\sqrt{5}\)
CM
20 tháng 2 2018
a)
3 x 2 − 5 x + 1 x 2 − 4 = 0 ⇔ 3 x 2 − 5 x + 1 = 0
hoặc x 2 – 4 = 0 ( 2 )
+ Giải (1): 3 x 2 – 5 x + 1 = 0
Có a = 3; b = -5; c = 1 ⇒ Δ = ( - 5 ) 2 – 4 . 3 = 13 > 0
Phương trình có hai nghiệm: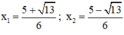 
+ Giải (2): x 2 – 4 = 0 ⇔ x 2 = 4 ⇔ x = 2 hoặc x = -2.
Vậy phương trình có tập nghiệm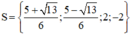 
b)
2 x 2 + x − 4 2 − ( 2 x − 1 ) 2 = 0 ⇔ 2 x 2 + x − 4 − 2 x + 1 2 x 2 + x − 4 + 2 x − 1 = 0 ⇔ 2 x 2 − x − 3 2 x 2 + 3 x − 5 = 0 ⇔ 2 x 2 − x − 3 = 0 ( 1 )
hoặc 2 x 2 + 3 x – 5 = 0 ( 2 )
+ Giải (1): 2 x 2 – x – 3 = 0
Có a = 2; b = -1; c = -3 ⇒ a – b + c = 0
⇒ Phương trình có hai nghiệm x = -1 và x = -c/a = 3/2.
+ Giải (2): 2 x 2 + 3 x – 5 = 0
Có a = 2; b = 3; c = -5 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm x = 1 và x = c/a = -5/2.
Vậy phương trình có tập nghiệm 