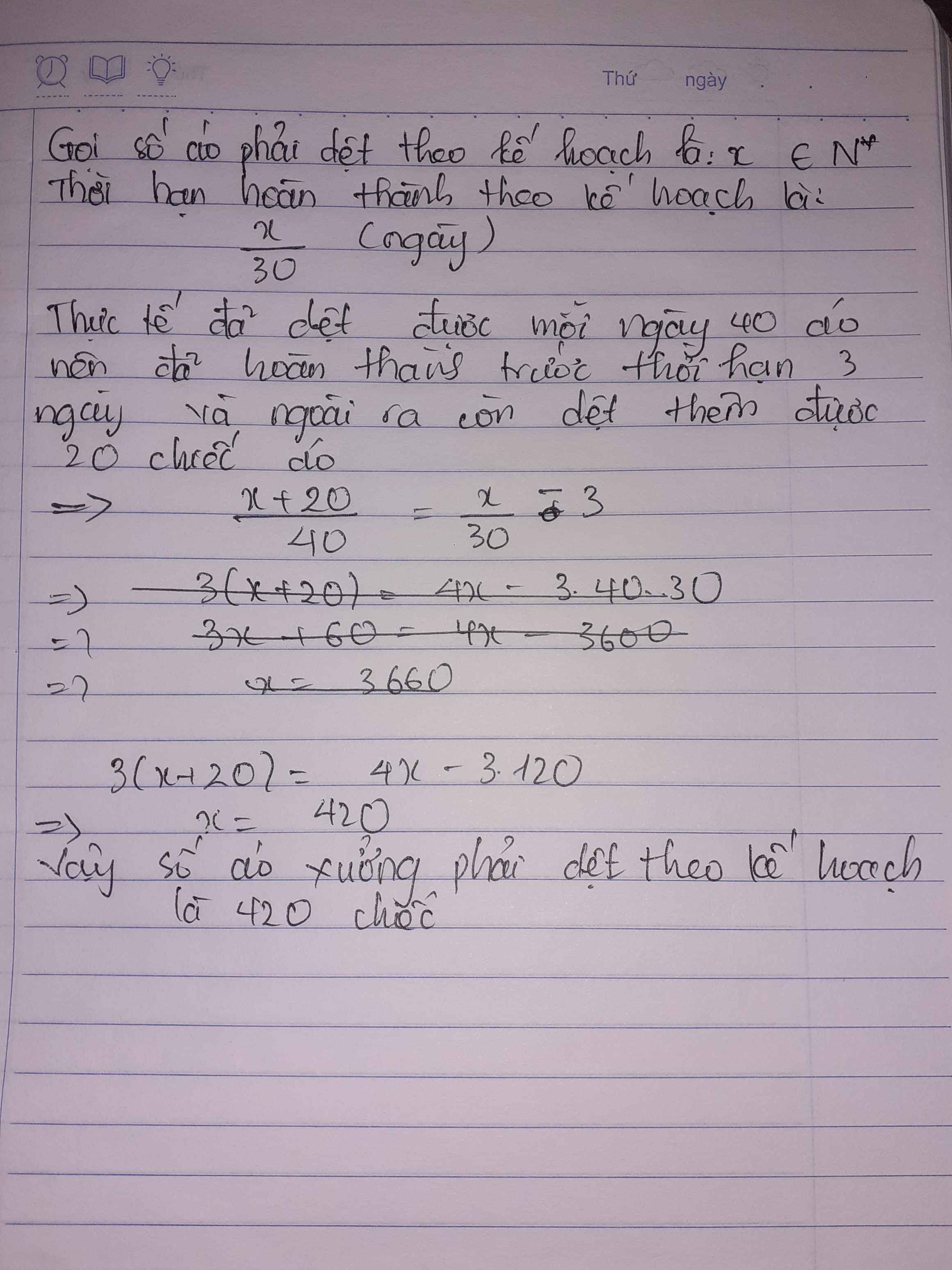Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi thời gian dự định để dệt hết số áo theo kế hoạch của xưởng là \(x\)(ngày )
Vì thực tế mỗi ngày dệt được 40 cái nên đã hoàn thành trước thời hạn 3 ngày, ngoài ra còn dệt thêm đươc 20 cái áo nên ta có phương trình:
\(40\left(x-3\right)-30x=20\)
⇔ \(40x-120-30x=20\)
⇔ \(10x-120=20\)
⇔ \(10x=140\)
⇒ \(x=14\) ( ngày )
Tổng số áo phải đệt theo kế hoạch là \(14.30=420\) ( áo )
Vậy số áo theo kế hoạch là \(420\) áo

Gọi thời gian xưởng làm theo kế hoạch là x (ngày, x > 30)
Tổng số áo theo kế hoạch là 30x (áo)
Vì đội hoàn thành trước thời hạn 3 ngày nên thời gian làm theo thực tế là x – 3 ngày
Vì theo thực tế đội làm thêm được 20 sản phẩm nên ta có phương trình
40(x – 3) = 30x + 20 ó 40(x – 3) – 20 = 30x.
Đáp án cần chọn là: D

Gọi số ngày may theo kế hoạch là x( ngày, x>0 )
Số áo phải may theo kế hoạch = 60x( áo )
Thực tế, phân xưởng may được 64 áo/ngày và hoàn thành kế hoạch trước 2 ngày
=> Số ngày phân xưởng thực hiện kế hoạch là x - 2 ( ngày ) và may được 64( x - 2 ) áo
Theo đề bài , số áo may được nhiều hơn so với kế hoạch là 140 áo
=> Ta có phương trình : 60x + 140 = 64( x - 2 )
<=> 60x + 140 = 64x - 128
<=> 60x - 64x = -128 - 140
<=> -4x = -268
<=> x = 67 ( tmđk )
=> Theo kế hoạch, phân xưởng phải may 67.60 = 4020 áo
Đ/s: 4020 áo
Gọi số áo phải dệt theo kế hoạch là x ( cái áo ) x > 0
=> Số ngày phải dệt là x/60 (ngày)
Số ngày dệt 64/ngày là x/64 (ngày)
Ta có : x/60 - x/64 = 2
<=> 64x x 60x = 7680
<=> x = 1920 (tm)
Nhưng vượt số lượng sản phẩm là 140 cái áo
=> Số áo phải dệt là :
1920 - 140 = 1780 ( cái áo )
Đó là cách giải bài toán này theo cách lập phương trình

gọi số áo phải dệt theo kế hoạch là x(cái áo) x>0
=> số ngày phải dệt là x/60(ngày)
số ngày dệt 64/ngày là x/64(ngày)
ta có x/60-x/64=2
<=> 64x-60x=7680
<=> x=1920(tm)
nhưng vượt số lượng sản phẩm là 140 cái áo
=> số áo phải dệt là 1920-140=1780 cái áo

Gọi số áo mà tổ cần may kế hoạch là \(x\) (chiếc). Điều kiện \(x \in {\mathbb{N}^*}\).
Vì ban đầu, tổ có ý định may 30 chiếc áo mỗi ngày nên thời gian dự định hoàn thành kế hoạch là \(\frac{x}{{30}}\) (ngày).
Thực tế, tổ đã may thêm được 20 chiếc áo nữa nên số áo tổ đã may được là \(x + 20\) (chiếc).
Vì thực tế mỗi ngày may được 40 chiếc áo nên thời gian tổ đã may áo là \(\frac{{x + 20}}{{40}}\) (ngày)
Vì tổ hoàn thành kế hoạch sớm hơn 3 ngày nên ta có phương trình:
\(\frac{x}{{30}} - \frac{{x + 20}}{{40}} = 3\)
\(\frac{{4.x}}{{30.4}} - \frac{{\left( {x + 20} \right).3}}{{3.40}} = \frac{{120.3}}{{120}}\)
\(\frac{{4x}}{{120}} - \frac{{3x + 60}}{{120}} = \frac{{360}}{{120}}\)
\(4x - \left( {3x + 60} \right) = 360\)
\(4x - 3x - 60 = 360\)
\(x = 360 + 60\)
\(x = 420\) (thỏa mãn)
Vậy theo kế hoạch tổ cần may 420 chiếc áo.

gọi số áo tổ đó phải may theo kế hoạch là: x(chiếc)(x>0)
theo kế hoạch tổ đó hoàn thành trong \(\dfrac{x}{30}\)(ngày)
thực tế tổ đó làm trong: \(\dfrac{x+20}{40}\left(ngay\right)\)
hoàn tành trước thời hạn 3 ngày
\(=>\dfrac{x}{30}-\dfrac{x+20}{40}=3=>x=420\left(TM\right)\)
Vậy theo kế haoch tổ đó phải may 420 chiếc áo

Gọi số áo tổ đó phải may theo kế hoạch là a (a \(\in\) N*)
Số áo tổ đó đã may trong thực tế là a + 20
Số ngày tổ đó may theo kế hoạch là \(\frac{a}{30}\)
Số ngày tổ đó may trong thực tế là \(\frac{a+20}{40}\)
Ta có \(\frac{a}{30}=\frac{a+20}{40}+3\)
\(\Leftrightarrow4a=3\left(a+20\right)+360\)
\(\Leftrightarrow4a=3a+60+360\)
\(\Leftrightarrow4a-3a=60+360\)
\(\Leftrightarrow a=420\)
Vậy số áo tổ đó phải may theo kế hoạch là 420