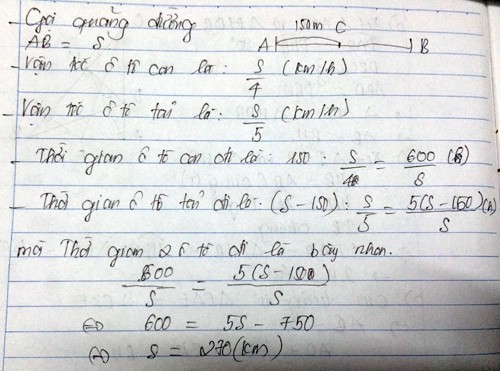Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Một giờ ô tô đi được:
\(\dfrac{3}{5}\cdot100=60\left(km\right)\)
Vận tốc của ô tô là:
\(60:1=60\left(km/h\right)\)
Một giờ xe máy đi được:
\(\dfrac{1}{2}\times100=50\left(km\right)\)
Vận tốc của ô tô là:
\(50:1=50\left(km/h\right)\)
Tổng vậy tốc của hai xe là:
\(60+50=110\left(km/h\right)\)
Hai xe gặp nhau sau:
\(100:110\approx0,9\left(h\right)\)
Đổi: \(0,9\left(h\right)=54\) phút
Ta thấy: 54 phút > 45 phút
Nên hai xe chạy 45 phút vẫn chữa gặp nhau

Gọi x và y là vận tốc của xe con và xe tải.
x.4=5.y=AB=> x=5y/4 (1)
Hai ze đi với thời gian như nhau nên (t=S/v)
150/x=(AB-150)/y
<=>AB=(150y/x)+150=5y
<=> 30y+30x=xy (2)
Thay (1) vào (2):
30y+ (30.6y)/4=5y^2/4
<=> 24y+30y=y^2
<=> y(y-54)=0
<=> y=0 (loại)
or y=54=> AB=5.54=270 (km)

Gọi vận tốc của xe ô tô thứ nhất, thứ 2 lần lượt là a; b (km/h; a;b > 0)
Gọi độ dài quãng đường AB là: S (km; S > 0)
Như vậy, a = S/12; b = S/14
Gọi quãng đường xe thứ nhất, thứ hai đi được đến khi 2 xe gặp nhau lần lượt là x;y (km; x;y > 0)
=> x + y = S
Vì thời gian 2 xe đi để gặp nhau như nhau nên vận tốc và quãng đường là 2 đại lượng tỉ lệ thuận
=> S/12 : S/14 = x/y = 14/12 = 7/6
=> x/7 = y/6
Áp dụng t/c của dãy tỉ số = nhau ta có:
x/7 = y/6 = x+y/7+6 = S/13 = 520/13 = 40
=> x = 40.7 = 280
Vậy quãng đường ô tô thứ nhất đi được đến khi gặp ô tô thứ 2 hay khoảng cách từ A đến nơi 2 ô tô gặp nhau là 280 km
dài quá, cần tiết kiệm t để thi toán trắc nghiệm đh sau này, " học là cho mk mà"

Ta có: 45 phút = 0,75 giờ
Gọi thời gian xe máy đi từ B đến C là x (giờ, x > 0,75)
Thời gian ô tô đi từ B đến C là: x - 0,75
Khi đó quãng đường BC = 40x = 50(x - 0,75)
<=> 40x = 50x - 37,5
<=> 50x - 40x = 37,5
<=> 10x = 37,5 <=> x = 3,75 (giờ)
Quãng đường BC là: 40 . 3,75 = 150 (km)
Vậy quãng đường BC dài 150km