Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Tính chất chuyển động của xe: xe đang chuyển động đều thì gặp chướng ngại vật, xe chuyển động chậm dần
- Mối liên hệ về hướng của vận tốc và gia tốc
+ Bắt đầu rời bến, xe chuyển động đều: a và v cùng hướng
+ Xe chuyển động chậm dần đều: a và v cùng phương nhưng ngược chiều.

Giải: Chọn chiều dương là chiều chuyển động của xe máy, gốc tọa độ tại vị trí hãm phanh, gốc thời gian là lúc hãm hanh
Ta có v 0 = 54 3 , 6 = 15 m / s xe dừng lại sau 10s nên v 1 = 0 m / s
v 1 = v 0 + a t ⇒ a = v 1 − v 0 t = 0 − 15 10 = − 1 , 5 m / s 2
Vận tốc của oto sau khi hãm phanh được 6s v 6 = v 0 + a t 6 ⇒ v 6 = 15 − 1 , 5.6 = 6 m / s

Chọn đáp án D
Lời giải:
+ Chọn chiều dương là chiều chuyển động của xe máy, gốc tọa độ tại vị trí hãm phanh, gốc thời gian là lúc hãm hanh
Ta có v 0 = 54 3 , 6 = 15 m / s xe dừng lại sau 10s nên v 1 = 0 m / s
v 1 = v 0 + a t ⇒ a = v 1 − v 0 t = 0 − 15 10 = − 1 , 5 m / s 2
Vận tốc của oto sau khi hãm phanh được 6s v 6 = v 0 + a t 6 ⇒ v 6 = 15 − 1 , 5.6 = 6 m / s

Đáp án A
Do khoảng thời gian ∆t thì xe chuyển động được quãng đường ∆s=v0.∆t=20∆t
Do đó, khi người lái xe bắt đầu hãm phanh thì khoảng cách giữa xe và chướng ngại vật là: s = 100 - 20∆Mà khi xe bị hãm phanh thì quãng đường xe còn chuyển động được đến khi dừng hẳn là:
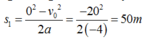
Vậy để xe không va vào chướng ngại vật thì
![]()
![]()

Đáp án B
Chọn trục tọa độ Ox có chiều trùng cới chiều chuyển động của người đi xe máy và xe buýt, chiều dương hướng từ người đi xe máy đến xe buýt. Gốc O tại vị trí xuất phát của người đi xe máy. Gốc thời gian là lúc người và xe buýt bắt đầu chuyển động.
Tại thời điểm t:
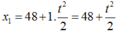
Vị trí của xe buýt :
![]()
Vị trí của người đi xe máy:
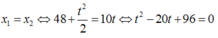
Khi người đi xe máy bắt kị xe buýt thì
![]()
Như vật thời gian nhỏ nhất để người đi xe máy bắt kịp xe buýt là 8 s, sau đó người đi xe máy sẽ vượt lên xe buýt. Tại t2 = 12s xe buýt sẽ lại đuổi kịp xe máy. Sau thời điểm này, xe buýt luôn ở trước xe máy.

Đổi 72 km/h=20m/s
Gia tốc của xe là
ta có: \(a=\dfrac{v^2-v_0^2}{2s}=\dfrac{0-20^2}{2\cdot50}=-4\left(\dfrac{m}{s^2}\right)\)
Phương trình chuyển động của xe
\(x=v_0t+\dfrac{1}{2}at^2=20t-2t^2\left(m,s\right)\)

- Tính chất chuyển động của xe: xe đang chuyển động đều thì gặp chướng ngại vật, xe chuyển động chậm dần
- Mối liên hệ về hướng của vận tốc và gia tốc
+ Bắt đầu rời bến, xe chuyển động đều: a và v cùng hướng
+ Xe chuyển động chậm dần đều: a và v cùng phương nhưng ngược chiều.