
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


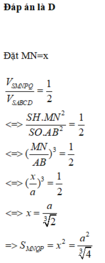

Đáp án B.
Trước hết ta có kết quả: Khối tứ diện ABCD có thể tích được tính theo công thức
![]()
Áp dụng kết quả này, ta có
![]()
= 6h
trong đó MN = PQ = 6 dm và h = d(MN;PQ) là chiều cao của hình trụ.
Từ giả thiết ta có h = 5 dm
Suy ra thể tích khối trụ là ![]() , với r = 3 dm
, với r = 3 dm
Do đó thể tích của lượng đá bị cắt bỏ là
![]()
Vậy phương án đúng là B.
Phân tích phương án nhiễu.
Phương án A và C: Sai do HS giải đúng nhưng làm tròn số bị sai hoặc lấy
Phương án D: Sai do HS chọn π = 3,141

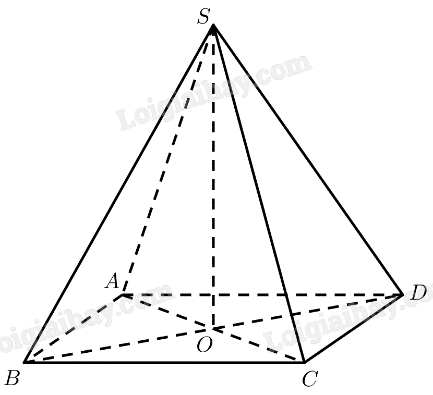
Mô hình hoá đèn đá muối bằng hình chóp tứ giác đều \(S.ABC{\rm{D}}\).
Gọi \(O\) là tâm của đáy.
\(\Delta SAC\) cân tại \(S\) \( \Rightarrow SO \bot AC\)
\(\Delta SBD\) cân tại \(S\) \( \Rightarrow SO \bot B{\rm{D}}\)
\( \Rightarrow SO \bot \left( {ABCD} \right)\)
\(ABCD\) là hình vuông \( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \Rightarrow AO = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SAO\) vuông tại \(O \Rightarrow SO = \sqrt {S{A^2} - A{O^2}} = \frac{{a\sqrt 2 }}{2}\)
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = A{B^2} = {a^2}\\{V_{S.ABC{\rm{D}}}} = \frac{1}{3}.{S_{ABC{\rm{D}}}}.SO = \frac{{{a^3}\sqrt 2 }}{6}\end{array}\)

Đáp án A
Đặt a> 0 cạnh hình vuông là Dễ thấy
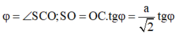
Gọi O là tâm của đáy. Vẽ AH ⊥ SC tại, H, AH cắt SO tại I thì A I O ^ = φ
![]()
Qua I vẽ đường thẳng song song DB cắt SD, SB theo thứ tự tại K, L. Thiết diện chính là tứ giác
ALHK và tứ giác này có hai đường chéo AH ⊥ KL Suy ra
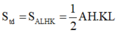
Ta có:


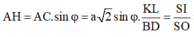
![]()
Theo giả thiết
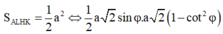
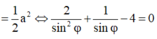
Giải được
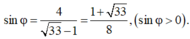
Suy ra φ = a r c sin 33 + 1 8