Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Khoảng thời gian ngắn nhất giữa hai lần động năng bằng thế năng:
∆ t = T 4 = π 10 ⇒ T = 2 π 5 ( s ) ⇒ ω = 5 ( r a d / s )
Vị trí động năng bằng thế năng( W d = W t )
![]()
Tại vị trí đó, gia tốc có độ lớn 2 m/ s 2 nên
![]()
Cơ năng của vật: W = 1 2 m ω 2 A 2 = 1 2 0 , 25 . 5 2 . ( 0 , 08 2 ) 2 = 0 , 04 J = 40 m J

\(T/4=0,15 \Rightarrow T=0,6s\)
Áp dụng định luật bảo toàn năng lượng từ thời điểm khảo sát cho đến thời gian t:
\( W_đ+W_t = 3W_đ + \dfrac{W_t}{3} \Rightarrow \dfrac{2}{3}.W_t=2W_đ \Rightarrow W_t=3W_đ
\)\(\Rightarrow x_1=A.\dfrac{\sqrt{3}}{2} \Rightarrow x_2=\dfrac{A}{2}
\)
Suy ra thời gian chuyển động từ \(x_1\) đến \(x_2\) là \(\dfrac{T}{12}\)
\(\Rightarrow v_{tb}=\frac{S}{T/12}=73,2cm\)

Đáp án A
Ta có 1 ô ⇔ 0 , 4 s ⇒ 1 ô = 0,1 s
![]()
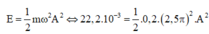
=> A = 0,06 m = 6 cm
Thấy 2 đỉnh của D 1 v à D 2 cách nhau 2 ô (1T là 8 ô)=> D 1 v à D 2 vuông pha:
A 2 = A 1 2 + A 2 2 ⇒ A 2 = 6 2 - 3 2 = 3 3 = 5 , 19 c m

- Ta có: 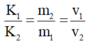
- Từ đồ thị ta thấy: A1 = 3 cm.
- Cũng theo đồ thị thì ta thấy cứ một ô ngang theo trục thời gian là 0,1s.
- Quan sát đồ thị ta thấy thời gian dao động D2 đi từ VTCB ra biên mất thời gian là 2 ô nên:
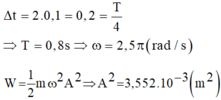
- Gọi Δ1 là thời gian kể từ lúc D1 bắt đầu dao động đến khi lần đầu tiên qua VTCB:
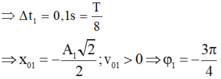
- Gọi Δ2 là thời gian kể từ lúc D2 bắt đầu dao động đến khi lần đầu tiên đến biên âm:
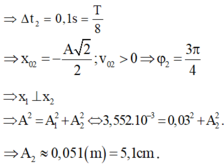

Đáp án A
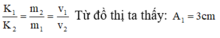
Cũng theo đồ thị thì ta thấy cứ một ô ngang theo trục thời gian là 0,1s
Quan sát đồ thị ta thấy thời gian dao động D 2 đi từ VTCB ra biên mất thời gian là 2 ô nên :
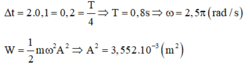
Gọi ∆ t 1 là thời gian kể từ lúc D 1 bắt đầu dao động đến khi lần đầu tiên qua VTCB:
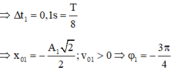
Gọi ∆ t 2 là thời gian kể từ lúc D 2 bắt đầu dao động đến khi lần đầu tiên đến biên âm