Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\omega=2\pi/T=\pi(rad/s)\)
Giả sử PT dao động là: \(x=A\cos(\pi t)(cm)\)
Suy ra: \(v=-\pi.A\sin(\pi t)\)
Tại thời điểm t ta có: \(A\cos(\pi t)=2\)
Tại thời điểm t + 0,5s thì vận tốc là:
\(v=-\pi.A\sin[\pi(t+0,5)]=-\pi.A\sin(\pi t +0,5\pi)\)
\(\Rightarrow v = -\pi.A\cos(\pi t)=-\pi.2=-2\pi(cm/s)\)
Chọn đáp án D.

Tai thời điểm t = 0,5s ta có
Li độ: x = 24.cos( π .0,5/2 + π ) = 24cos5 π /4 = -16,9 ≈ 17 cm
Vận tốc : v = - 24. π /2.sin( π .0,5/2 + π ) = -24.π/2.sin5 π /4 = 6 π 2 cm/s = 26,64 cm/s ≈ 27 cm/s
Gia tốc : a = - π / 2 2 .x = - π / 2 2 .(-16,9) = 41,6 cm/ s 2 ≈ 42 (cm/ s 2 )

Đáp án A
+ Ta để ý rằng, trong dao động điều hòa thì li độ và vận tốc luôn vuông pha nhau
+ Hai thời điểm t 1 và t 2 vuông pha nhau do vậy v 2 sẽ ngược pha với x 1 , ta có v 2 x 1 = b x 1 = ω = π rad.
Tương tự, thời điểm t 3 ngược pha với t 2 nên ta có
v 3 v 2 = 1 ⇔ b + 8 π b = 1 ⇒ b + 8 π b = − 1 ⇒ b = − 4 π
Thay vào biểu thức trên ta tìm được x 1 = 4 cm

Chọn đáp án C
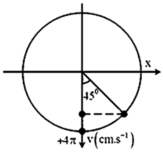
Vận tốc cực đại của dao động:
v max = ω A = 4 π c m / s .
Tại thời điểm t = 0,25 s vật có vận tốc:
v = 2 2 v max = 2 π 2 c m / s .
Biễu diễn các vị trí tương ứng trên đường tròn.
Ta thu được: φ 0 = − π 2 r a d .
Phương trình dao động của vật là:
x = 4 cos π t − π 2 c m .

Đáp án C

Vận tốc cực đại của dao động a m a x = ω A = 4 π cm / s
Tại thời điểm t = 0,25 s vật có vận tốc v = 2 2 x m a x = 2 π 2 cm / s
Tại thời điểm t=0 ứng với góc lùi ∆ φ = ω ∆ t = 0 , 25 π
Biễu diễn các vị trí tương ứng trên đường tròn. Ta thu được φ 0 = - π 2 r a d
Phương trình dao động của vật là x = 4 cos ( πt - π 2 ) c m




T=2s=>ω=π
Công thức độc lập thời gian
\(\dfrac{x^2}{A^2}+\dfrac{v^2}{\omega^2A^2}=1\)
=>A2=x2+\(\dfrac{v^2}{\omega^2}\)
=>A=\(\dfrac{2\sqrt{55}}{5}\)
x=\(\dfrac{2\sqrt{55}}{5}\)cos(πt)=2
Th1 t=0,26s=>t'=0,6s=>v=-8,8cm/s
Th2 t=-0,26s=>t'=0,07s=>v=-2,03cm/s