Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

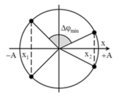
Quãng đường không đổi (6cm) nên để thời gian đi ngắn nhất thì tốc độ của vật phải lớn nhất, do đó vật dao động 1 đoạn 6cm đối xứng quanh VTCB.
Biểu diễn trạng thái trên bằng véc tơ quay ta được:
Vật đi quãng đường 6cm ứng với véc tơ quay từ M đến N.
Góc quay $\alpha = 2.30^0 = 60^0$
Suy ra thời gian: $t=\dfrac{60}{360}T=\dfrac{T}{6}=\dfrac{1}{3}s$

Ta có: \(W_đ=W_t\Rightarrow x =\pm\dfrac{A}{\sqrt 2}\)
Như vậy, để \(W_t < W_đ\) thì: \(|x| <\dfrac{A}{\sqrt 2}\)
Biểu điễn bằng véc tơ quay, ta tìm đc khoảng thời gian tương ứng này bằng T/4 = 2/4 = 0,5s
Chọn A.

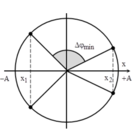
Góc quay được trong 1/3 giây là;
\(\text{Δ}\varphi=\omega\cdot\text{Δ}t=\dfrac{2pi}{T}\cdot\text{Δ}t=\dfrac{2pi}{3}\cdot\dfrac{1}{3}=\dfrac{2pi}{6}=\dfrac{pi}{3}\)
Độ dài quãng đường lớn nhất vật đi được trong 1/3 giây là;
\(S_{max}=2\cdot A\cdot sin\left(\dfrac{pi}{3}:2\right)=2\cdot A\cdot sin\left(\dfrac{pi}{6}\right)=A\)(m)
Để tính quảng đường dài nhất mà vật đi được trong 1/3s, chúng ta có thể sử dụng công thức quảng đường dài nhất của vật dao động điều hoà: Smax = A. Trong trường hợp này, vật dao động điều hoà với chu kỳ T = 2s và biên độ A. Vì vậy, quảng đường dài nhất mà vật đi được trong 1/3s là A.