Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Biên độ A = 10/2=5cm.
- Vật đi 5cm mà chưa đổi chiều chuyển động đến li độ 2,5cm suy ra vật đi từ li độ -2,5cm đến 2,5cm.
- Biểu diễn bằng véc tơ quay.
-5 5 -2,5 2,5 M N
Ứng với véc tơ quay từ M đến N
Góc quay là \(60^0\)
Thời gian: \(t=\dfrac{60}{360}T=0,5\Rightarrow T = 3s\)
Tần số \(f=\dfrac{1}{T}=1/3(Hz)\)
Chọn A nhé bạn.

Lời giải:
Vì tại thời điểm ban đầu vật đang qua VTCB theo chiều âm nên phương trình dao động của vật \(x=A\cos\left(\omega t+\frac{\pi}{2}\right)\) (cm)
Từ điều kiện đề bài kết hợp với công thức \(A^2=x^2+\left(\frac{v}{\omega}\right)^2\) nên \(\omega=2\pi\Rightarrow A=5\left(cm\right)\)
Do đó phương trình là \(x=5\cos\left(2\pi t+\frac{\pi}{2}\right)\left(cm\right)\)

Pha ban đầu bằng 0 --> Vật xuất phát từ biên độ dương.
10 5 M N
Như vậy, lần đầu tiên (lẻ) vật qua li độ 5cm ứng với véc tơ quay đến M, và lần thứ 2 (chẵn) ứng với véc tơ quay đến N.
Cứ như vậy, thời gian để vật qua li độ 5cm lần 2015 đến 2016 ứng với véc tơ quay từ M đến N.
Góc quay 2400
Thời gian: \(t=\dfrac{240}{360}T=\dfrac{2}{3}.0,2=\dfrac{2}{15}s\)

Bạn áp dụng CT của dao động điều hòa:
\(A^2=x^2+\dfrac{v^2}{\omega^2}\)
Với \(x=\alpha.\ell\), li độ là độ dài cung của góc \(\alpha\) (tính theo rad)
\(\Rightarrow (\alpha_0.\ell)^2=(\alpha.\ell)^2+\dfrac{v^2.\ell}{g}\)
\(\Rightarrow \alpha_0^2=\alpha^2+\dfrac{v^2}{g\ell}\)
Chọn đáp án A.

Phương pháp: Áp dụng định luật bảo toàn động lượng
Cách giải:
Gọi vận tốc của hệ ngay sau khi va chạm là v. Áp dụng định luật bảo toàn động lượng ta có:

Đáp án A

Đáp án A
Vị trí có li độ x = 2 2 A vật có E d = E t = 0 , 5 E = 0 , 25 m ω 2 A 2 .
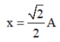
Đáp án A