Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Xét
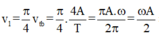
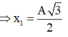
Vùng tốc độ ≥ v 1 nằm trong - x 1 ; x 1
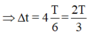 kết hợp với bài ta có T=0,5(s)
kết hợp với bài ta có T=0,5(s)
Phân tích 1 6 = T 3 quãng đường lớn nhất vật đi được trong T 3 khi vật đi qua lân cận vị trí cân bằng
Công thức
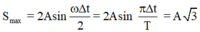 ,
,
đối chiếu với giả thiết ta có A=2(cm)
Vận tốc cực đại của vật trong quá trình chuyển động
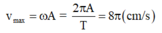

Đáp án A
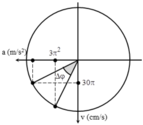
+ Biểu diễn các vị trí tương ứng trên đường tròn. Để thõa mãn điều kiện bài toán thì khoảng thời 1 60 s gian tương ứng với góc quét Δφ
→ Từ hình vẽ, ta có:
arcos 30 π ωA − arsin 300 π 2 ω 2 A 360 0 T = arcos 30 π 6 ω − arsin 300 π 2 6 ω 2 ω = 1 60
→ Phương trình trên cho ta nghiệm ω = 31,6 rad/s → T = 0,2 s

Đáp án C
+ Cứ mỗi khoảng thời gian

![]()
vật lại có tốc độ

![]()
Tốc độ trung bình của vật trong một chu kì
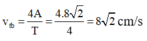

Đáp án C
(a) Chu kì của dao động là T = 2 π ω = 2 s → ( a ) s a i
(b) Tốc độ cực đại của chất điểm là v m a x = ω . A = 18 , 8 c m / s → ( b ) đ ú n g
(c) Gia tốc của chất điểm có độ lớn cực đại là a m a x = ω 2 A = 59 , 2 c m / s 2 → ( c ) sai
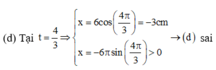
(e) Tốc độ trung bình của vật trong một chu kì dao động là v t b = 4 A T = 12 c m / s → ( e ) đ ú n g
(f) Tốc độ trung bình của vật trong một nửa chu kì dao động là v t b = 2 A 0 , 5 T = 12 c m / s → (f) sai
(g) Trong 0,25T vật có thể đi được quãng đường
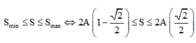
![]()

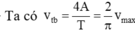
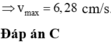





Chọn đáp án C.
Xét vùng v 1 = π 4 v tb = π 4 . 4A T = πAω 2π = ωA 2 ⇒ x 1 = A 3 2
Vùng tốc độ ≥ v 1 khi vật chuyển động từ − x 1 đến x 1 ( hình vẽ)
⇒ Δ t = 4 T 6 = 2T 3 kết hợp với bài ta có T = 0 , 5 ( s )
Phân tích 1 6 = T 3 , quãng đuờng lớn nhất vật đi đuơc trong T/3 khi vật đi qua lân cận vị trí cân bằng
Công thức s max = 2Asin ωΔt 2 = 2Asin πΔt T = A 3 , đối chiếu với giả thiết ta có A = 2(cm)
Vận tốc cực đại của vật trong quá trình chuyển động:
v max = ωA = 2πA T = 8π(cm/s)