


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Đáp án A
Xét thiết diện của vật thể cắt bởi mặt phẳng vuông góc với Ox tại điểm x là nửa elip có bán trục lớn bằng 2 x , do đó có bán trục nhỏ bằng x (do trục lớn gấp đôi trục nhỏ)
Suy ra diện tích của thiết diện tại điểm x là S x = 1 2 . π .2 x . x = π x
Vậy thiết diện của vật thể là V = ∫ 0 4 π x d x = π x 2 2 4 0 = 8 π . Chọn đáp án A

Ta có diện tích thiết diện là
S ( x ) = 1 2 πR 2 = 1 2 πx 2 4 - x = 1 2 π 4 x 2 - x 3
Thể tích của vật thể cần tìm là
V = ∫ 0 4 S ( x ) d x = 1 2 π ∫ 0 4 4 x 2 - x 3 dx = 1 2 π 4 3 x 3 - 1 4 x 4 | 0 4 = 32 π 3
Chọn đáp án D.

Chọn đáp án A
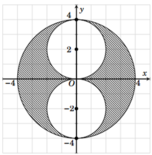
Hình phẳng H 1 được biểu diễn bằng miền tô đậm trong hình vẽ bên.
Thể tích khối trụ bán kính r = 4 chiều cao h = 8 là V = πr 2 h = 128 π đvtt
Thể tích của khối tròn xoay thu được khi quay hình phẳng giới hạn bởi parabol y = x 2 4 trục hoành, đường thẳng y = 4 xung quanh trục tung là

Suy ra thể tích của khối tròn xoay thu được khi quay H 1 quanh trục Oy là:
V 1 = V - 2 V P = 64 π (đvtt).
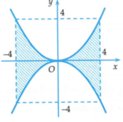
* Hình phẳng H 2 được biểu diễn bằng miền tô đậm trong hình vẽ bên.
Thể tích khối cầu lớn bán kính R = 4 là V L = 4 3 π . R 3 = 256 π 3 (đvtt)
Thể tích khối cầu nhỏ bán kính r = 2 là V N = 4 3 πr 3 = 32 π 3
Suy ra thể tích của khối tròn xoay thu được khi quay H 2 quanh trục Oy là
![]()
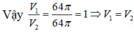

Đáp án B

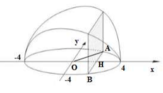
V 1 bằng thể tích khối trụ có bán kính đáy bằng 4 và chiều cao bằng 8 trừ bốn lần thể tích của vật tròn xoay tạo thành khi vật thể giới hạn bởi các đường x = 2 y , x = 0 , y = 0 , x = 4 quay quanh trục Oy
. V 1 = π .4 2 .8 − 4 π ∫ 0 4 2 y d y = 64 π . Thể tích
V 2 = 4 3 π ( 4 3 − 2 3 − 2 3 ) = 64 π .