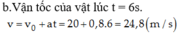Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3. Quãng đường vật đi từ thời điểm t1=1s đến thời điểm t2=2s:
\(S=S_2-S_1=30+4\cdot2-2^2-\left(30+4\cdot1-1^2\right)=1m\)
4. \(v=36\)km/h=10m/s
Gia tốc vật: \(v=v_0+at\Rightarrow a=0,8\)m/s2

Câu a bn tính s trong 5s - s trong 2s là ra dc s can tìm tiep theo lay t2-t1 ra dc t trung binh tính Vtb bằng Stb : Ttb Câu b áp dụng công thức v bằng Vo cộng at thế a bằng 4 Vo bằng 20( ở pt gốc) và t bằng 3s vào là ra
Câu b ap dung cthuc v bằng Vo cộng at thế Vo bằng 20 (lấy ở pt gốc

Giải: Ta có phương trình quãng đường: s = 20 t + 0 , 2 t 2
Quãng đường vật đi được t 1 = 2 s : S 1 = 20.2 + 0 , 2.2 2 = 40 , 8 m
Quãng đường vật đi được t 2 = 5 s : S 2 = 20.5 + 0 , 2.5 2 = 105 m
Quãng đường vật đi được từ thời điểm t 1 = 2 s đến thời điểm t 2 = 5 s : Δ S = S 2 − S 1 = 105 − 40 , 8 = 64 , 2 m
Vận tốc trung bình v = Δ x Δ t = x 2 − x 1 t 2 − t 1
Tọa độ vật đi được t 1 = 2 s : x 1 = 10 + 20.2 + 0 , 2.2 2 = 50 , 8 m
Tọa độ vật đi được t 2 = 5 s : x 2 = 10 + 20.5 + 0 , 2.5 2 = 115 m
Vận tốc trung bình v = x 2 − x 1 t 2 − t 1 = 115 − 50 , 8 5 − 2 = 21 , 4 ( m / s )
b.Vận tốc của vật lúc t = 3s. v = v 0 + a t = 5 + 0 , 4.3 = 6 , 2 m / s

Ta có phương trình quãng đường:

Quãng đường vật đi được từ thời điểm t1 = 1s đến thời điểm t2 = 4s:
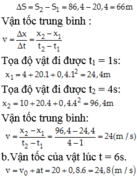

a,Phương trình chuyển động của vật
\(x=4t^2+20t\left(cm,s\right)\Rightarrow a=8\left(\dfrac{cm}{s^2}\right);v_0=20\left(\dfrac{cm}{s}\right)\)
Vậy vận tốc ban đầu của vật là 20 cm/s và gia tốc của vật là 8 cm/s2
b, Vận tốc của vật ở thời điểm t=2s
\(v=20+8\cdot2=36\left(\dfrac{cm}{s}\right)\)
Vị trí của vật ở thời điểm t=2s cách gốc tọa độ 1 khoảng
\(x=4\cdot2^2+20\cdot2=56\left(cm\right)\)
c,Quãng đường đi được trong khoảng thời gian 5 s kể từ lúc chuyển động là
\(s=4\cdot5^2+20\cdot5=200\left(cm\right)\)
d Vận tốc trung bình trong khoảng thời gian từ t1=2s đến t2=5s
Ta có:\(x_1=4\cdot2^2+20\cdot2=56\left(cm\right)\)
\(x_2=4\cdot5^2+20\cdot5=200\left(cm\right)\)
\(v_{tb}=\dfrac{x_2-x_1}{t_2-t_1}=\dfrac{200-56}{5-2}=48\left(\dfrac{cm}{s}\right)\)