Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vật đã đi được 4s
\(v=9-2t\Rightarrow\left\{{}\begin{matrix}v_0=9\\a=-2\end{matrix}\right.\)
\(S=v_0t+\dfrac{1}{2}at^2=20m\)

Đáp án C
Từ phương trình vận tốc suy ra :
Chú ý: Có thể tính bằng công thức vtb như sau
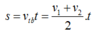
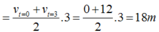

Quãng đường vật chuyển động: \(S=v_0t+\dfrac{1}{2}at^2=20t+\dfrac{1}{2}at^2\)
Vật chuyển động chậm dần đều \((a=0m/s^2)\) cho đến khi vật dừng lại \((v=0m/s)\).
\(v^2-v_0^2=2aS\Rightarrow S=\dfrac{-20^2}{2\cdot a}=-\dfrac{200}{a}\left(m\right)\)
\(\Rightarrow20t+\dfrac{1}{2}at^2=-\dfrac{200}{a}\)
Mà \(v=v_0+at=20+at=0\Rightarrow a=-\dfrac{20}{t}\)
Như vậy: \(\Rightarrow20t+\dfrac{1}{2}\cdot\left(-\dfrac{20}{t}\right)\cdot t^2=-\dfrac{200}{-\dfrac{20}{t}}\)
\(\Rightarrow t=1272,7s\)
Gia tốc vật: \(a=-\dfrac{20}{1272,7}\approx-0,0157m/s^2\)

Theo kết quả trên, ta tìm được quãng đường vật đi được sau khoảng thời gian t = 10 s là
s 10 = 5.10 + (0.2. 10 2 )/2 = 50 + 10 = 60 (m)