Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu: \(C_{10}^3\)
Số cách chọn sao cho có 2 nữ 1 nam là: \(C_6^2.C_4^1\)
Xác suất: \(P=\dfrac{C_6^2.C_4^1}{C_{10}^3}=\dfrac{1}{2}\)

Không gian mẫu:
Chọn 5 người từ 15 người để lập nhóm 1 có \(C_{15}^5\) cách, chọn 5 người từ 10 người còn lại để lập nhóm 2 có \(C_{10}^5\) cách, tổ 3 có \(C_5^5\) cách
\(\Rightarrow C_{15}^5.C_{10}^5.C_5^5\) cách chọn bất kì
Bây giờ ta tính số cách chia sao cho có ít nhất 1 nhóm không có nữ:
Do 7 nữ luôn chia được vào ít nhất 2 nhóm sao cho mỗi nhóm có 5 người, do đó chỉ có nhiều nhất 1 nhóm (trong số 3 nhóm) chỉ toàn là nam.
Chọn 1 nhóm từ 3 nhóm để xếp 5 nam: \(C_3^1\) cách
Chọn 5 nam từ 8 nam để xếp vào nhóm nói trên: \(C_8^5\) cách
Còn 10 em xếp vào 2 nhóm còn lại: \(C_{10}^5.C_5^5\) cách
\(\Rightarrow C_3^1.C_8^5.C_{10}^5.C_5^5\) cách xếp sao cho có 1 ít nhất nhóm ko có nữ
\(\Rightarrow C_{15}^5.C_{10}^5.C_5^5-C_3^1.C_8^5.C_{10}^5.C_5^5\) cách xếp thỏa mãn
Xác suất: ...
Anh ơi! Câu này làm theo cách biến cố đối, hai học sinh nữ đứng cạnh nhau thì như nào ạ, em làm được trực tiếp còn làm gián tiếp không được ạ.
https://hoc24.vn/cau-hoi/doi-tuyen-hoc-sinh-gioi-cua-mot-truong-thpt-co-8-hoc-sinh-nam-va-4-hoc-sinh-nu-trong-buoi-le-trao-phan-thuong-cac-hoc-sinh-tren-duoc-xep-thanh-mot-hang-ngang-tinh-xac-suat-de-khi-xep-sao-cho-2-hoc.7929973126107

Q(x)=x^5(3x-5)^7
Số hạng chứa x^10 sẽ tương ứng với số hạng chứa x^5 trong (3x-5)^7
SHTQ là: \(C^k_7\cdot\left(3x\right)^{7-k}\cdot\left(-5\right)^k=C^k_7\cdot3^{7-k}\cdot\left(-5\right)^k\cdot x^{7-k}\)
Số hạng chứa x^5 tương ứng với 7-k=5
=>k=2
=>Số hạng cần tìm là: 127575x^10

Ta có: n(Ω)=C515=3003�(Ω)=�155=3003
Gọi A là biến cố "Trong 5 học sinh được chọn có ít nhất 4 học sinh nữ".
Ta có thể chọn 4 nữ và 1 nam hoặc chon 5 nữ.
Suy ra n(A)=C49.C16+C59=882�(�)=�94.�61+�95=882
Xác suất của biển cố A là: P(A)=8823003=42143≈0,29
Ta có: n(Ω)=C515=3003�(Ω)=�155=3003
Gọi A là biến cố "Trong 5 học sinh được chọn có ít nhất 4 học sinh nữ".
Ta có thể chọn 4 nữ và 1 nam hoặc chon 5 nữ.
Suy ra n(A)=C49.C16+C59=882�(�)=�94.�61+�95=882
Xác suất của biển cố A là: P(A)=8823003=42143≈0,29

a) Số cách chọn ba học sinh bất kì là: \(C_{40}^3 = 9880\)
b) Số cách chọn ba học sinh gồm 1 nam và 2 nữ là: \(C_{25}^1.C_{15}^2 = 2625\)
c) Số cách chọn 3 học sinh trong đó không có học sinh nam là: \(C_{15}^3 = 455\)
Số cách chọn 3 học sinh trong đó có ít nhất một học sinh nam là: \(9880 - 455 = 9425\)

a: Số cách chọn là: \(C^3_{25}=2300\left(cách\right)\)
b: Số cách chọn là: \(C^1_{15}\cdot C^2_{24}=4140\left(cách\right)\)

Không gian mẫu: \(12!\)
Xếp 8 nam: có \(8!\) cách
8 nam tạo thành 9 khe trống, xếp 4 nữ vào 9 khe trống này: \(A_9^4\) cách
\(\Rightarrow8!.A_9^4\) cách
Xác suất: \(P=\dfrac{8!.A_9^4}{12!}=\)
Câu này có thể coi như không giải theo cách gián tiếp được (thực ra là có giải được nhưng ko ai giải kiểu đó hết), nó bao gồm các trường hợp 4 nữ cạnh nhau, 3 nữ cạnh nhau, 2 nữ cạnh nhau, trong đó trường hợp trước còn bao hàm trường hợp sau cần loại trừ nữa

Chọn hai học sinh từ tổ sao cho 2 học sinh cùng giới có 2 công đoạn
\(CD_1:\) Chọn 1 bạn nữ trong 5 bạn nữ \(\Rightarrow\) Có 5 cách chọn
\(CD_2:\) Chọn 1 bạn nam trong 4 bạn nam \(\Rightarrow\) Có 4 cách chọn
Áp dụng quy tắc nhân, ta có : \(5.4=20\) ( cách chọn )
Vậy có 20 cách chọn 2 học sinh từ tổ để 1 bàn có 2 học sinh cùng giới
Lời giải:
Chọn 2 học sinh cùng giới tính nam, có: $C^2_4=6$ cách
Chọn 2 học sinh cùng giới tính nữ, có: $C^2_5=10$ cách
Tổng số cách chọn: $6+10=16$ (cách)
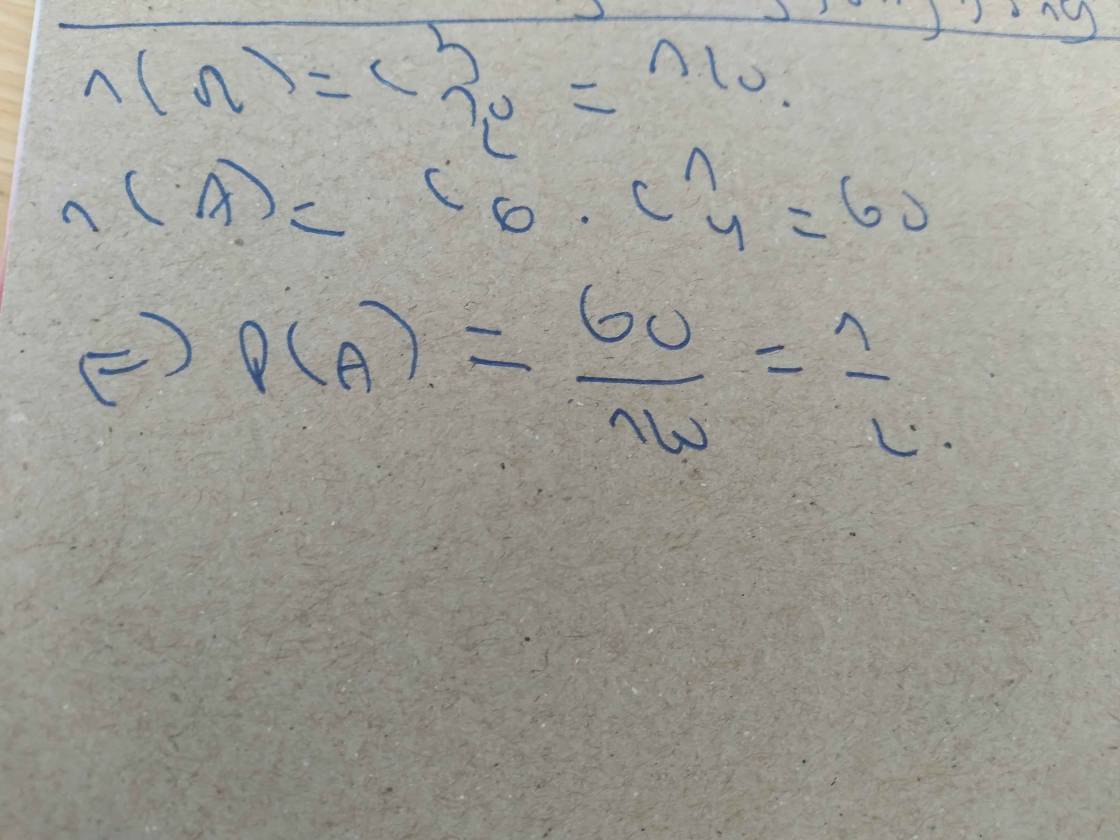
\(\Omega \) là tập tất cả 6 học sinh trong 12 học sinh. Vậy \(n\left( \Omega \right) = C_{12}^6 = 924\).
Gọi C là biến cố: “Có 3 học sinh nam và 3 học sinh nữ”. Có \(C_7^3\) cách chọn chọn 3 học sinh nam và \(C_5^3\) cách chọn 3 học sinh nữ. Theo quy tắc nhân, ta có \(C_7^3.C_5^3 = 350\) cách chọn 3 học sinh nam và 3 học sinh nữ tức là \(n\left( C \right) = 350\).Vậy \(P\left( C \right) = \frac{{350}}{{924}} \approx 0,3788\).