Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

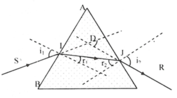
a) Áp dụng công thức lăng kính ta có:
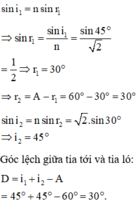
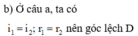
tính được ở câu a, là góc lệch cực tiểu. Do đó nếu ta tăng hoặc giảm góc tới 10 ° thì góc lệch tăng.

Do tính đối xứng nên:
r 1 = r 2 = A 2 = 30 ° i 1 = i 2 = A + D 2 = 60 + 30 2 = 45 °
Ta có: sin i 1 = n sin r 1 ⇒ n = sin i 1 sin r 1 = sin 45 0 sin 30 0 = 2 2. 1 2 = 2

Do tính đối xứng nên: r 1 = r 2 = A 2 = 30 °
Ta có: sin i 1 = n sin r 1 . Thế số: sin i 1 = n sin r 1 = 2 sin 30 0 = 2 2 = > i 1 = 45 0 = i 2
Góc lệch: D = i 1 + i 2 - A = 45 + 45 - 60 = 30 °

Đáp án cần chọn là: C
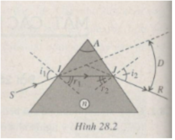
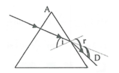
Tia sáng chiếu tới AB vuông góc tại H nên truyền thẳng tới AC tại K
Xét tam giác AHK vuông tại H có = 30 0 → AKH ^ = 60 0 → i = 30 0 (1)
Ta có, tại mặt bên AC: sin i g h = 1 n = 1 2 → i g h = 45 0 (2)
Từ (1) và (2): i < sin i g h → tia sáng truyền tại mặt bên AC tại K bị khúc xạ ra ngoài không khí với góc lệch D như hình vẽ: D = r – i (3)
Áp dụng định luật khúc xạ ánh sáng tại mặt AC ta có:
n . sin i = sinr → 2 sin 30 = sinr → sinr = 2 2 → r = 45 0
Thay vào (3) → D = 15 0
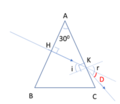

Đáp án cần chọn là: B
Theo bài ra: i 1 = 45 0 , n = 2
sin i 1 = n sin r 1 ⇒ sin 45 0 = 2 sin r 1 ⇒ r 1 = 30 0 ⇒ r 2 = A – r 1 = 30 0
n sin r 2 = sin i 2 ⇒ 2 sin 30 0 = sin i 2 ⇒ i 2 = 45 0
Góc lệch: D = ( i 1 + i 2 ) – A = 30 0

a) Góc lệch có giá trị cực tiểu khi: 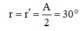
Áp dụng định luật khúc xạ ánh sáng ta có:



Đáp án cần chọn là: A
Vì chiếu tia tới vuông góc với mặt nên i 1 = 0 → r 1 = 0
Ta có: A = r 1 + r 2 → A = r 2
Mà: D = i 1 + i 2 − A ↔ 15 = 0 + i 2 − A → i 2 = 15 + A
Lại có:
sin i 2 = n sinr 2 ↔ sin i 2 = n sin A ↔ sin ( 15 + A ) = 1,5 sin A
↔ sin 15 c osA + sinAcos 15 = 1,5 sin A
↔ sin 15 c osA = ( 1,5 − cos 15 ) sinA
→ tan A = sin 15 1,5 − c os 15 = 0,485 → A = 25,87

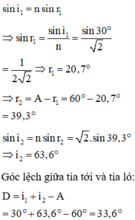
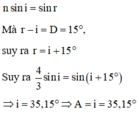
Đáp án C