Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Coi hai bờ sông lần lượt là đường thẳng \({d_1},{d_2}.\) Giả sử tàu 1 xuất phát từ A hướng về hạ lưu và tàu 2 xuất phát từ B hướng về thượng nguồn như hình vẽ.
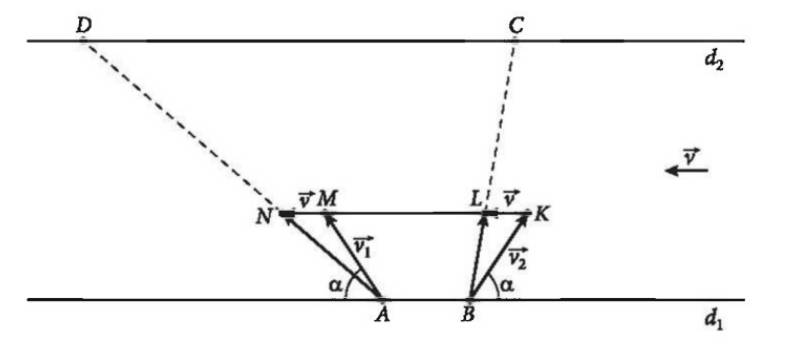
Ta sử dụng các vecto \(\overrightarrow v ,\overrightarrow {{v_1}} ,\overrightarrow {{v_2}} \) để biểu diễn cho vận tốc của dòng nước, vận tốc riêng của tàu 1 và tàu 2.
Lấy các điểm K, M sao cho \(\overrightarrow {BK} = \overrightarrow {{v_2}} ,\overrightarrow {AM} = \overrightarrow {{v_1}} .\) Từ giả thiết suy ra tứ giác ABKM là một hình thang cân.
Lấy các điểm L, N sao cho \(\overrightarrow {KL} = \overrightarrow v = \overrightarrow {MN} \). Khi đó K, L, M, N cùng nằm trên một đường thẳng song song với \({d_1},{d_2}\) và các vecto \(\overrightarrow {AN} = \overrightarrow {{v_1}} + \overrightarrow v ,\overrightarrow {BL} = \overrightarrow {{v_2}} + \overrightarrow v \) tương ứng biểu diễn cho vận tốc thực của tàu 1 và tàu 2.
Khi đó tàu 1 chuyển động theo hướng \(\overrightarrow {AN} \) đến đích là điểm D. Tàu 2 theo hướng \(\overrightarrow {BL} \) đến đích là điểm C.
Do các đường thẳng KL, MN, \({d_1},{d_2}\) đôi một song song nên theo định lí Ta-lét ta có: \(\frac{{AD}}{{AN}} = \frac{{BC}}{{BL}} = k\).
Trong đó AD, AN là quãng đường đi và độ lớn vận tốc của tàu 1 còn BC, BL là quãng đường đi và độ lớn vận tốc của tàu 2.
Như vậy hai tàu cần thời gian như nhau để sang bờ bên kia.
Vậy hai tàu sang đến bờ bên kia cùng một lúc.

Chọn C.
Sau 2h quãng đường tàu thứ nhất chạy được là: S1 = 30.2 = 60km
Sau 2h quãng đường tàu thứ hai chạy được là: S2= 40.2 = 80 km
Suy ra sau 2h hai tàu cách nhau là:
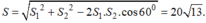

Sau 2h tàu thứ nhất ở vị trí B cách A là: \(2.30=60\left(km\right)\)
Tàu thứ 2 ở vị trí C cách A là: \(2.40=80\left(km\right)\)
Áp dụng định lý hàm cos:
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cos60^0}=20\sqrt{13}\approx72,1\left(km\right)\)

a)
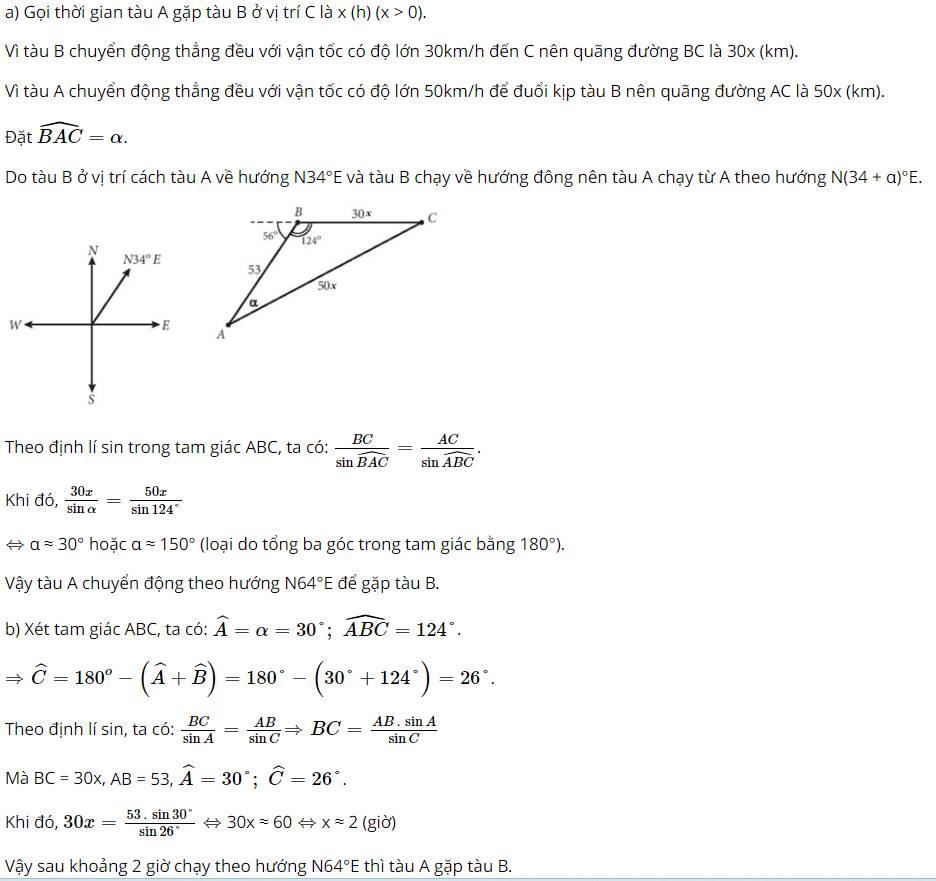
Gọi t (đơn vị: giờ) là thời gian đi cho đến khi hai tàu gặp nhau tại C.
Tàu B đi với vận tốc có độ lớn 30km/h nên quãng đường BC = 30t
Tàu A đi với vận tốc có độ lớn 50km/h nên quãng đường AC = 50t
Theo định lí sin, ta có: \(\frac{a}{{\sin \alpha }} = \frac{b}{{\sin B}}\)
Trong đó: \(\left\{ \begin{array}{l}a = BC = 30t\\b = AC = 50t\\\widehat B = {124^o}\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \frac{{30t}}{{\sin \alpha }} = \frac{{50t}}{{\sin {{124}^o}}}\\ \Leftrightarrow \sin \alpha = \frac{{30t.\sin {{124}^o}}}{{50t}} = \frac{{30.\sin {{124}^o}}}{{50}} \approx 0,4974\end{array}\)
\( \Leftrightarrow \alpha \approx {30^o}\) hoặc \(\alpha \approx {150^o}\)(loại)
Vậy tàu A chuyển động theo hướng tạo với vị trí ban đầu của tàu B góc \({30^o}\).
b) Xét tam giác ABC, ta có:
\(\begin{array}{l}\widehat B = {124^o};\widehat A = {30^o}\\ \Rightarrow \widehat C = {180^o} - \left( {\widehat B + \widehat A} \right) = {180^o} - \left( {{{124}^o} + {{30}^o}} \right) = {26^o}\end{array}\)
Theo định lí sin, ta có
\(\frac{a}{{\sin A}} = \frac{c}{{\sin C}} \Rightarrow a = \frac{{c.\sin A}}{{\sin C}}\)
Mà \(\left\{ \begin{array}{l}a = BC = 30t\\c = AB = 53\\\widehat A = {30^o};\widehat C = {26^o}\end{array} \right. \Rightarrow 30t = \frac{{53.\sin {{30}^o}}}{{\sin {{26}^o}}}\)
\(\begin{array}{l} \Leftrightarrow 30t \approx 60,45\\ \Leftrightarrow t \approx 2\;(h)\end{array}\)
Vậy sau khoảng 2 giờ thì tàu A đuổi kịp tàu B.

Giải tam giác là việc đi tìm một số yếu tố của tam giác khi đã biết các yếu tố khác của tam giác đó.
Trong trường hợp này, giải tam giác ABC được hiểu là tìm cạnh AC khi biết cạnh AB, góc A và góc B.
Áp dụng định lí sin ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
Mà \(AB=d, \hat {B} =\beta; \hat {C} =180^o-\alpha -\beta \)
\(\Rightarrow AC = \sin \beta \frac{d}{{\sin \left( {{{180}^o} - \alpha - \beta } \right)}}\)

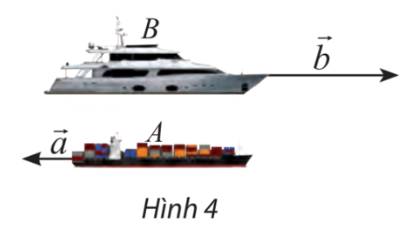
Ta thấy hai hướng đông và tây là ngược nhau và tỉ số độ dài \(\frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{50}}{{20}} = \frac{5}{2}\)
\( \Rightarrow \overrightarrow b = - \frac{5}{2}\overrightarrow a \)


Sự khác biệt là:
- Đơn vị đo: tấn và 500.
- Khối lượng hàng là đại lượng chỉ có độ lớn (500 tấn), còn độ dịch chuyển của tàu là đại lượng có cả độ lớn (500 km) và hướng (từ A đến B).
Gọi E là vị trí ban đầu người đó đứng, AC là khoảng cách từ mặt nước đến đáy con tàu bị đắm dưới nước
=>Chiều sâu của con tàu đắm sẽ là EC=EA+AC
Gọi B là vị trí mà người đó lặng xuống sao cho khoảng cách từ điểm đó đến vị trí con tàu đắm là 14m, CD là độ dài của con tàu
Kẻ Ax\(\perp\)EC tại A, By\(\perp\)EC tại B
=>Ax//By
Theo đề, ta có: CD\(\perp\)CE tại C, BE=14m; AE=8m; \(\widehat{xAD}=70^0\); \(\widehat{yBD}=57^0\)
By\(\perp\)EC
CD\(\perp\)EC
Do đó: By//CD
mà By//Ax
nên Ax//By//CD
By//CD
=>\(\widehat{yBD}=\widehat{BDC}\)(hai góc so le trong)
mà \(\widehat{yBD}=57^0\)
nên \(\widehat{BDC}=57^0\)
Xét ΔBCD có \(\widehat{ABD}\) là góc ngoài tại B
nên \(\widehat{ABD}=\widehat{BCD}+\widehat{BDC}=90^0+57^0=147^0\)
\(\widehat{xAD}+\widehat{BAD}=\widehat{xAB}=90^0\)
=>\(\widehat{BAD}=90^0-\widehat{xAD}=90^0-70^0=20^0\)
Xét ΔBAD có \(\widehat{BAD}+\widehat{ABD}+\widehat{ADB}=180^0\)
=>\(\widehat{ADB}=180^0-147^0-20^0=13^0\)
Xét ΔBCD vuông tại C có \(sinBDC=\dfrac{BC}{BD}\)
=>\(\dfrac{14}{BD}=sin57\)
=>\(BD=\dfrac{14}{sin57}\simeq16,69\left(m\right)\)
Xét ΔBAD có \(\dfrac{BD}{sinBAD}=\dfrac{AB}{sinADB}\)
=>\(\dfrac{AB}{sin13}=\dfrac{16.69}{sin20}\)
=>\(AB\simeq10,98\left(m\right)\)
Chiều sâu con tàu đắm là:
EC=EA+AC=8+10,98+14=32,98(m)