Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sơ đồ tạo ảnh
AB → A’B’
d d’
Công thức thấu kính: 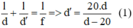
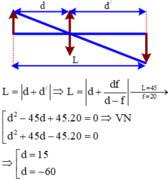
Gọi khoảng cách từ vật tới ảnh là L ⇒ |d’ + d| = L.
Vật thật ⇒ d > 0
L = 45cm
∗ Trường hợp 1
d’ + d = -45cm (2)
Từ (1) và (2) ta có:
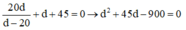
Giải phương trình lấy nghiệm d > 0 ta được: d = 15 cm
∗ Trường hợp 2
d’ + d = 45cm (3)
Từ (1) và (3) ta có:
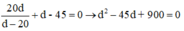
phương trình này vô nghiệm

a)Độ tụ của thấu kính:
\(D=\dfrac{1}{f}=\dfrac{1}{20}\)
b)\(d=60cm\Rightarrow\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow d'=30cm\)
\(\Rightarrow\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow h'=1cm\)
Các trường hợp sau tương tự nhé.

a) \(D=\dfrac{1}{f}=\dfrac{1}{40}\)
b) Khi d = 20 cm
\(d'=\dfrac{d.f}{d-f}=\dfrac{20.40}{20-40}=-40\left(cm\right)\)
\(k=-\dfrac{d'}{d}=\dfrac{40}{20}=2\)
=> Ảnh ảo, cùng chiều và lớn hơn vật 2 lần.

Đáp án cần chọn là: A
Sử dụng công thức thấu kính: 1 f = 1 d + 1 d '
Thay số 1 10 = 1 20 + 1 d ' → d ' = 20 ( c m )

Đáp án cần chọn là: D
Gọi d là khoảng cách từ vật đến thấu kính
d 1 ' là khoảng cách từ ảnh của vật qua thấu kính hội tụ đến thấu kính
d 2 ' là khoảng cách từ ảnh của vật qua thấu kính phân kì đến thấu kính
Ta có:
+ Khi dùng thấu kính hội tụ: 1 f = 1 d + 1 d 1 ' ⇔ 1 f = 1 d + 1 60 (1)
+ Khi dùng thấu kính phân kì: 1 − f = 1 d + 1 d 2 ' ⇔ 1 − f = 1 d + 1 − 12 (2)
Lấy (1) – (2) ta được:
2 f = 1 60 + 1 12 ⇒ f = 20 c m
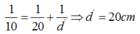
Sơ đồ tạo ảnh
AB → A’B’
d d’
Công thức thấu kính: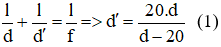
Gọi khoảng cách từ vật tới ảnh là L ⇒ |d’ + d| = L.
Vật thật ⇒ d > 0
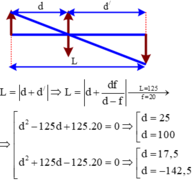
L = 125cm
∗ Trường hợp 1: A’B’ là ảnh thật → d’ > 0
→ L = d’ + d =125cm (2)
Từ (1) và (2) ta có:
Giải phương trình lấy nghiệm d1 > 0 ta được: d1 = 17,54 cm
∗ Trường hợp 2
d’ + d = - 125cm (trường hợp này thì ảnh A’B’ là ảnh ảo) (3)
Từ (1) và (3) ta có:
Giải phương trình lấy nghiệm d > 0 ta được: d = 25cm hoặc d = 100cm