Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
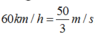
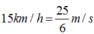
Sử dụng công thức
![]()
Giai đoạn tàu chuyển động từ vận tốc 60 km/h giảm xuống còn 15 km/h:
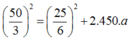
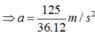
Gia đoạn tàu chuyển động từ 15 km/h tới khi dừng lại hẳn:
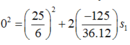
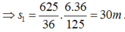
.

Chọn
Chiều dương là chiều chuyển động của tàu,
Gốc tọa độ tại vị trí hãm phanh
Gốc thời gian lúc bắt đầu hãm phanh.
a. Gia tốc của đoàn tàu là
\(v^2-v_o^2=2as\\ \Rightarrow a=\dfrac{5^2-20^2}{2.450}=-\dfrac{5}{12}\left(m/s^2\right)\)
b. Thời gian đi được quãng đường trên là
\(a=\dfrac{v-v_o}{t}\Rightarrow t=\dfrac{5-20}{-\dfrac{5}{12}}=36\left(s\right)\)
c. Thời gian khi xe hãm phanh và dừng hẳn là
\(a=\dfrac{v_1-v_0}{t}\Rightarrow t=\dfrac{0-5}{-\dfrac{5}{12}}=12\left(s\right)\)
Quãng đường xe đi được khi xe hãm phanh và dừng hẳn là
\(S=v_o.t+\dfrac{a}{2}.t^2=5.12.-\dfrac{5}{12}:2.12^2=-1800\left(m\right)\)

Chọn chiều dương là chiều chuyển động.
a) Gia tốc: a = v − v 0 Δ t = 0 − 12 2 , 5.60 = − 0 , 08 m/s2.
b) Từ v 2 − v 0 2 = 2 a s ⇒ quãng đường tàu đi được trong thời gian hãm:
s = v 2 − v 0 2 2 a = 0 − 12 2 2. ( − 0 , 08 ) = 900 (m).

a) Ta có: v0 = 43,2 km/h = 12 m/s; v = 0 m/s; t = 1 phút = 60 s.
Gia tốc của tàu là:
\(a = \frac{{v - {v_0}}}{t} = \frac{{0 - 12}}{{60}} = - 0,2(m/{s^2})\)
b) Quãng đường mà tàu đi được là:
\(d = \frac{{{v^2} - v_0^2}}{{2.a}} = \frac{{0 - {{12}^2}}}{{2.( - 0,2)}} = 360(m)\)

Đổi 54km/h = 15m/s; 1p = 60s
Gia tốc của tàu là:
Ta có: \(v=v_0+at\Leftrightarrow a=\dfrac{v-v_0}{t}=\dfrac{0-15}{60}=-0,25\left(m/s^2\right)\)

Đáp án D
Vật chuyển động chậm dần đều nên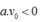
Do đó:
Chú ý: Khi đầu bài cho độ lớn gia tốc thì phải phân tích ( dựa vào dấu của v0 ) để biết dấu của a nó là âm hay dương