Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn chiều chuyển động ban đầu của quả cầu A là chiều dương. Hệ vật gồm hai quả cầu A và B. Gọi v 1 , v 2 và v ' 1 , v ' 2 là vận tốc của hai quả cầu trước và sau khi va chạm.
Vì hệ vật chuyển động không ma sát và ngoại lực tác dụng lên hệ vật (gồm trọng lực và phản lực của máng ngang) đều cân bằng nhau theo phương thẳng đứng, nên tổng động lượng của hệ vật theo phương ngang được bảo toàn (viết theo trị đại số):
m 1 v ' 1 + m 2 v ' 2 = m 1 v 1 + m 2 v 2
2. v ' 1 + 3. v ' 2 = 2.3 +3.1 = 9
Hay v ' 1 + 1,5. v ' 2 = 4,5 ⇒ v ' 2 = 3 - 2 v ' 1 /3 (1)
Đồng thời, tổng động năng của hệ vật cũng bảo toàn, nên ta có:
m1 v ' 1 2 /2 + m2 v ' 2 2 /2 = m1 v 1 2 /2 + m2 v 2 2 /2
2 v ' 1 2 /2 + 3 v ' 2 2 /2 = 2. 3 2 /2 + 3. 1 2 /2
Hay v ' 1 2 + 1,5 v ' 2 2 = 10,5 ⇒ v ' 2 2 = 7 - 2 v ' 1 2 /3 (2)
Giải hệ phương trình (1), (2), ta tìm được: v ' 1 = 0,6 m/s; v ' 2 = 2,6 m/s
(Chú ý: Loại bỏ cặp nghiệm v ' 1 = 3 m/s, v ' 2 = 1 m/s, vì không thỏa mãn điều kiện v ' 2 > v 2 = 1 m/s)

Độ lớn động lượng trước và sau va chạm là: p = m.v = 0,06.28 = 1,68 (kg.m/s)
- Tính chất của vecto động lượng trước va chạm:
+ Hướng từ trái sang phải, hợp với phương ngang 1 góc 450
+ Độ lớn: p = 1,68 kg.m/s
- Tính chất của vecto động lượng sau va chạm:
+ Hướng từ phải sang trái, hợp với phương ngang 1 góc 450
+ Độ lớn: p = 1,68 kg.m/s

Độ lớn động lượng trước và sau va chạm là: p = m.v = 0,06.28 = 1,68 (kg.m/s)
- Tính chất của vecto động lượng trước va chạm:
+ Hướng từ trái sang phải, hợp với phương ngang 1 góc 450
+ Độ lớn: p = 1,68 kg.m/s
- Tính chất của vecto động lượng sau va chạm:
+ Hướng từ phải sang trái, hợp với phương ngang 1 góc 450
+ Độ lớn: p = 1,68 kg.m/s

Chọn chiều chuyển động ban đầu của quả cầu thứ nhất là chiều dương. Vì hệ vật gồm hai quả cầu chuyển động theo cùng phương ngang, nên tổng động lượng của hệ vật này có giá trị đại số bằng :
Trước va cham : p 0 = m 1 v 1 + m 2 v 2
Sau va chạm : p = m 1 v ' 1 + m 2 v ' 2
Áp dụng định luật bảo toàn động lượng, ta có :
p = p 0 ⇒ m 1 v ' 1 + m 2 v ' 2 = m 1 v 1 + m 2 v 2
Suy ra: v ' 2 = (( m 1 v 1 + m 2 v 2 ) - m 1 v ' 1 )/ m 2
Thay v ' 1 = - 0,6 m/s, ta tìm được
v ' 2 = ((2.3 + 3.1) - 2.0,6)/3 = 2,6(m/s)
Quả cầu thứ hai chuyển động với vận tốc 2,6 m/s theo hướng ban đầu.

Với bài này bắt buộc bạn phải chọn chiều chuyển động thì mới xét được quả cầu thứ hai chuyển động như thế nào sau va chạm và xét định luật bảo toàn trong hệ kín. Trình bày:
Áp dụng định luật bảo toàn động lượng cho hệ kín hai quả cầu theo phương ngang: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p_1'}+\overrightarrow{p_2'}\)
Chọn chiều dương là chiều chuyển động ban đầu của quả cầu 1: ....
Động lượng của hệ trước khi bắn: \(p_0=m_1\upsilon_1+m_2\upsilon_2\)
Động lượng của hệ sau khi bắn: \(p=m_1\upsilon'_1+m_2\upsilon'_2\)
Theo định luật bảo toàn động lượng ta có:
\(p_0=p\)
\(\Leftrightarrow m_1\upsilon_1+m_2\upsilon_2=m_1\upsilon'_1+m_2\upsilon'_2\)
\(\Leftrightarrow3.1+2.3=3.1,2+2.\upsilon'_2\)
\(\Leftrightarrow3+6=3,6+2\upsilon'_2\)
\(\Leftrightarrow9=3,6+2\upsilon'_2\)
\(\Leftrightarrow2\upsilon'_2=9-3,6\)
\(\Leftrightarrow2\upsilon'_2=5,4\)
\(\Leftrightarrow\upsilon'_2=\dfrac{5,4}{2}=2,7m/s\)
Vậy tốc của quả cầu thứ hai là 2,7m/s và theo hướng ban đầu



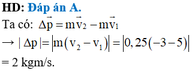
Chọn chiều dương là chiều chuyển động của quả cầu đập vào tường
Động lượng của quả cầu trước va chạm: p = m.v = 2.3,0 = 6,0 (kg.m/s)
Động lượng của quả cầu sau va chạm: p’ = -m.v’ = -2,3,0 = -6,0 (kg.m/s)
=> Động lượng của quả cầu sau va chạm giảm
Động năng của quả cầu trước va chạm là: \({W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}.2.{(3,0)^2} = 9,0(J)\)
Động năng của quả cầu sau va chạm là: \(W_d^; = \frac{1}{2}mv{'^2} = \frac{1}{2}.2.{( - 3,0)^2} = 9,0(J)\)
=> Động năng không thay đổi