Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc của xe máy là x (km/h; x > 0)
Vận tốc của ô tô là x + 24 (km/h)
Thời gian xe máy đi hết quãng đường là: 120/x (h)
Thời gian ô tô đi hết quãng đường là: 120/(x+4) (h)
Đổi 30 phút = 1/2 (h), 20 phút = 1/3 (h)
Theo đề bài ta có phương trình:
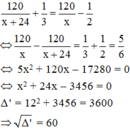
Phương trình có hai nghiệm x 1 = − 12 – 60 = −72 (loại) và x 2 = −12 + 60 = 48 (tmđk)
Vậy vận tốc xe máy là 48 km/h và vận tốc ô tô là 48 + 24 = 72 km/h
Đáp án: D

Thời gian ô tô đó đi từ A đến B ( không tính thời gian sửa xe là ) :
11 giờ 30 phút - 8 giờ - 15 phút = 3 giờ 15 phút = 13/4 giờ
Gọi vận tốc của ô tô đó là x ( km/h , x > 10 )
=> Vận tốc sau khi sửa xe = x - 10 ( km/h )
2/3 quãng đường là : 150 . 2/3 = 100(km)
=> Thời gian ô tô đi 2/3 quãng đường = 100/x ( giờ )
Độ dài quãng đường còn lại = 150 - 100 = 50(km)
=> Thời gian ô tô đi quãng đường còn lại = 50/x-10 ( giờ )
Tổng thời gian đi của ô tô là 13/4 giờ
=> Ta có phương trình : \(\frac{100}{x}+\frac{50}{x-10}=\frac{13}{4}\)
<=> \(\frac{100\cdot4\cdot\left(x-10\right)}{4x\left(x-10\right)}+\frac{50\cdot x\cdot4}{4x\left(x-10\right)}=\frac{13x\left(x-10\right)}{4x\left(x-10\right)}\)
<=> \(\frac{400\left(x-10\right)}{4x\left(x-10\right)}+\frac{200x}{4x\left(x-10\right)}=\frac{13x^2-130x}{4x\left(x-10\right)}\)
<=> \(\frac{400x-4000}{4x\left(x-10\right)}+\frac{200x}{4x\left(x-10\right)}=\frac{13x^2-130x}{4x\left(x-10\right)}\)
<=> 400x - 4000 + 200x = 13x2 - 130x
<=> 13x2 - 130x - 600x + 4000 = 0
<=> 13x2 - 730x + 4000 = 0 (1)
\(\Delta'=b'^2-ac=\left(-365\right)^2-13\cdot4000=133225-52000=81225\)
\(\Delta'>0\)nên (1) có hai nghiệm phân biệt
\(\hept{\begin{cases}x_1=\frac{-b'+\sqrt{\Delta'}}{a}=\frac{365+285}{13}=50\left(tm\right)\\x_2=\frac{-b'-\sqrt{\Delta'}}{a}=\frac{365-285}{13}=\frac{80}{13}\left(ktm\right)\end{cases}}\)
=> Vận tốc của ô tô = 50km/h
=> Thời gian người đó đi 2/3 quãng đường là : 100/50 = 2 ( giờ )
=> Ô tô hỏng lúc : 8 + 2 = 10 giờ
Đ/s : 10 giờ

Gọi vận tốc xe máy là x(km/h) với x>0
Vận tốc ô tô là: \(x+24\) (km/h)
Thời gian xe máy đi hết quãng đường AB là: \(\dfrac{120}{x}\) giờ
Thời gian ô tô đi hết quãng đường là: \(\dfrac{120}{x+24}\) giờ
Do xe máy xuất phát sau ô tô \(\dfrac{1}{2}\) giờ nhưng ô tô đến trước xe máy 1h20ph=\(\dfrac{4}{3}\) giờ nên thời gian ô tô đi ít hơn thời gian xe máy đi là \(\dfrac{4}{3}-\dfrac{1}{2}=\dfrac{5}{6}\) giờ
Ta có phương trình:
\(\dfrac{120}{x}-\dfrac{120}{x+24}=\dfrac{5}{6}\)
\(\Rightarrow720\left(x+24\right)-720x=5x\left(x+24\right)\)
\(\Leftrightarrow x^2+24x-576=0\) \(\Rightarrow\left[{}\begin{matrix}x=48\\x=-72\left(loại\right)\end{matrix}\right.\)
Vậy vận tốc xe máy là 48 (km/h) và vận tốc ô tô là 72 (km/h)

Gọi vận tốc xe máy là x(x>0) km/h
vận tốc ô tô là x+10
thời gian ô tô đi hết quãng đường \(\dfrac{120}{x}\)h
thời gian xe máy đi hết quãng đường là \(\dfrac{120}{x+10}\)h
thời gian xe máy đi trước ô tô là 6h10p-6h =10p =\(\dfrac{1}{6}\)h
vì xe ô tô đến trước xe máy 14p=\(\dfrac{7}{30}\)h nê ta có pt
\(\dfrac{120}{x}\)-\(\dfrac{120}{x+10}\)-\(\dfrac{1}{6}\)=\(\dfrac{7}{30}\)
giải pt x=50 tm
vậy vận tốc xe máy là 50km/h
vận tốc ô tô là 50+10=60km/h

Gọi vận tốc ban đầu là x km/h (x>o).
Với vận tốc này thì thời gian để đi quãng đường 30 km:
30/x(h)
Vì với vận tốc này sẽ đến B chậm mất nửa giờ hay chậm mất 1/2 h, nên suy ra thời gian dự định đến B sẽ là:
30/x - 1/2(h) (1)
Nếu tăng vận tốc thêm 5 km/h thì vận tốc mới sẽ là:
x + 5(km/h)
Với vận tốc mới thì thời gian đi hết 30 km sẽ là:
30/(x + 5)...(h)
Thời gian này so với thời gian dự định là sớm hơn nửa giờ (hay 1/2 h), nên suy ra thời gian dự định sẽ là:
30/(x + 5) +1/2 (h) (2)
Vì (1) bằng (2) nên ta có:
30/x - 1/2 = 30/(x + 5) +1/2
=> x^2 + 5x - 150 = 0
Giải phương trình trên ta có:
x1 = 10 (nhận)
x2 = - 15 (loại)
Vậy vận tốc ban đầu là 10 km/h.
Gọi v là vận tốc lúc đầu, t là thời gian chạy đoạn đường 30km.
Ta có: vt = 30 (1)
Người đó nhận thấy rằng sẽ đến B chậm mất nửa giờ nửa giữ nguyên vận tốc đang đi. Nhưng nếu tăng tốc thêm 5 km/h thì sẽ tới đích sớm hơn nửa giờ. => có nghĩa là nếu tăng v thêm 5 thì sẽ đi nhanh hơn 0.5 + 0.5 = 1h
Vậy ta có: (v + 5)(t - 1) = 30 (2)
Cho (1) = (2) => vt = vt + 5t - v - 5 <=> 5t - v - 5 = 0
thay t = 30/v vào ta có:
150/v - v - 5 =0
<=> 150 - 5v - v*v = 0
Lấy máy bấm => v = 10 (nhận) hoặc v = -15 (loại)

Gọi vận tốc ô tô là: x ( km/h ) ( x > 24 )
=) vận tốc xe máy là: x - 24 ( km/h )
Thời gian để ô tô đi hết quãng đường AB là: \(\frac{120}{x}\)( giờ )
Thời gian đẻ xe máy đi hết quãng đường AB là: \(\frac{120}{x-24}\)( giờ )
VÌ ô tô đến B được \(\frac{4}{3}\)giờ thì xe máy mới đén A cũng như ô tô đi trươc xe máy \(\frac{1}{2}\)giờ nên ta có phương trình:
\(\frac{120}{x-24}-\frac{4}{3}=\frac{120}{x}-\frac{1}{2}\)
\(\frac{120}{x-24}-\frac{120}{x}=\frac{5}{6}\)
\(\frac{720x}{6x.\left(x-24\right)}-\frac{720.\left(x-24\right)}{6x.\left(x-24\right)}=\frac{5x.\left(x-24\right)}{6x.\left(x-24\right)}\)
\(720x-720+17280=5x^2-120x\)
\(5x^2-120x-17280=0\)
\(x^2-24x-3456=0\)
\(\left(x-72\right).\left(x+48\right)=0\)
\(\orbr{\begin{cases}x=72\\x=-48\left(lo\text{ại}\right)\end{cases}}\)
Vận tốc ô tô là: 72 km/h
Vận tốc xe máy là: 48 km/h
Gọi vận tốc xe máy là x (km/h) (x>0)
thì vận tốc ô tô là: x + 24 (km/h)
Thời gian xe máy đi quãng đường AB là: \(\frac{120}{x}\)(h)
Thời gian ô tô đi quãng đường AB là:\(\frac{120}{x+24}\)(h)
Thời gian xe máy đi nhiều hơn ô tô: 1h20' - (7h30' - 7h) = 50' = \(\frac{5}{6}\) (h)
Ta có phương trình: \(\frac{120}{x}-\frac{120}{x+24}=\frac{5}{6}\)
<=> 6.[120(x+24) - 120x] = 5x(x+24)
<=> 720(x+24) - 720x = 5x^2 + 120x
<=> 5x^2 + 120x - 17280 = 0
<=> x = 48 (TMĐK) hoặc x = -72 (không TMĐK)
Vậy vận tốc xe máy là 48 km/h
vận tốc ô tô là: 48+24=72 (km/h)
Mọi người giải nhanh giúp mình với, thứ 6 là phải trả bài rối. Gấp lắm ạ!