Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số sản phẩm 1 ngày phải sản xuất là x
Thời gian dự kiến là 600/x
Thời gian thực tế là 400/x+200/(x+10)
Theo đề, ta có: \(\dfrac{600}{x}-\dfrac{400}{x}-\dfrac{200}{x+10}=1\)
=>\(\dfrac{200}{x}-\dfrac{200}{x+10}=1\)
=>(200x+2000-200x)=x^2+10x
=>x^2+10x-2000=0
=>x=40

| KLCV | Năng suất | Thời gian | |
| Kế hoạch | 1000 | x | \(\dfrac{1000}{x}\) |
| Thực tế | 1000+80=1080 | x+10 | \(\dfrac{1080}{x+10}\) |
Pt: \(\dfrac{1000}{x}-\dfrac{1080}{x+10}=2\)
Gọi số sản phẩm đội dự định làm mỗi ngày là x \(\left(x\in N,x< 100\right)\)( sản phẩm )
Theo kế hoạch
Thời gian hoàn thành là:\(\dfrac{1000}{x}\left(ngày\right)\)
Thực tế.
Mỗi ngày tổ làm được x+10 ( sản phẩm).
Thời gian hoàn thành : \(\dfrac{1080}{x+10}\)( ngày)
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
\(\dfrac{1000}{x}-\dfrac{1080}{x+10}=2\)
\(\Leftrightarrow\dfrac{500}{x}-\dfrac{540}{x+10}=1\) ( quy đồng đơn giản hơn để dễ làm )
\(\Leftrightarrow\dfrac{500.\left(x+10\right)-540x}{x\left(x+10\right)}=\dfrac{x\left(x+10\right)}{x\left(x+10\right)}\)
\(\Leftrightarrow500x+5000-540x=x^2+10x\) (quy đồng bỏ mẫu )
\(\Leftrightarrow x^2+50x-5000=0\)
\(\Leftrightarrow\) pt có 2 nghiệm phân biệt
th1 : x=-100 ( vô lí)
th2 x= 50 ( nhận )
Vậy...
Gọi \(x\) (ngày) là số ngày hoàn thành theo kế hoạch (\(x\) > 2)
Số sản phẩm mỗi ngày theo kế hoạch: \(\dfrac{1000}{x}\) (sản phẩm)
Số sản phẩm mỗi ngày thực làm: \(\dfrac{1000}{x}+10\)
Số ngày thực làm: \(x-2\) (ngày)
Theo đề bài ta có phương trình:
\(\left(\dfrac{1000}{x}+10\right).\left(x-2\right)=1080\)
\(\Leftrightarrow1000-\dfrac{2000}{x}+10x-20=1080\)
\(\Leftrightarrow10x^2+980x-1080x-2000=0\)
\(\Leftrightarrow10x^2-100x-2000=0\)
\(\Leftrightarrow x^2-10x-200=0\)
\(\Leftrightarrow x^2-20x+10x-200=0\)
\(\Leftrightarrow\left(x^2-20x\right)+\left(10x-200\right)=0\)
\(\Leftrightarrow x\left(x-20\right)+10\left(x-20\right)=0\)
\(\Leftrightarrow\left(x-20\right)\left(x+10\right)=0\)
\(\Leftrightarrow x-20=0;x+10=0\)
*) \(x-20=0\)
\(\Leftrightarrow x=20\) (nhận)
*) \(x+10=0\)
\(x=-10\) (loại)
Vậy số sản phẩm theo kế hoạch đội đó phải làm trong một ngày là: \(\dfrac{1000}{20}=50\) (sản phẩm)

Gọi số sản phẩm tổ dự định làm theo kế hoạch là x (sản phẩm, ![]() ).
).
Thiết lập được PT:
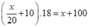
Từ đó tìm được x = 800 (sản phẩm)

Gọi x(sản phẩm) là số sản phẩm tổ 1 phải làm theo kế hoạch
đk: 0<x<800,x∈Z+
800-x(sản phẩm) là số sản phẩm tổ 2 phải làm theo kế hoạch
0,1x(sản phẩm ) là số sản phẩm tổ 1 làm thêm được
0,2(800-x) (sản phẩm ) là số sản phẩm tổ 2 làm thêm được
Vì cả 2 tổ làm thêm được 910-800=110(sản phẩm) nên ta có phương trình:
0,1x+0,2(800−x)=1100,1x+0,2(800−x)=110
⇔0,1x−160−0,2x=110⇔0,1x−160−0,2x=110
⇔0,1x=50⇔0,1x=50
⇔x=500(tmđk)⇔x=500(tmđk)
Vậy theo kế hoạch, tổ 1 phải làm 500 sản phẩm
tổ 2 phải làm 800-500=300 sản phẩm

Gọi số sản phẩm tổ 1 làm là x
Số sản phẩm tổ 2 làm là 1000-x
Theo đề, ta có: \(\dfrac{11}{10}x+\dfrac{6}{5}\left(1000-x\right)=1140\)
=>x=600
Vậy: Tổ 1 cần làm 600 sản phẩm
Tổ 2 cần làm 400 sản phẩm

Thực tế tổ sản xuất làm được số sản phẩm mỗi ngày là: 30 + (30 : 100 x 10) = 33 (sản phẩm)
Gọi số ngày dự định hoàn thành xong tất cả sản phẩm là x (ngày, x > 2)
Số ngày thực tế hoàn thành xong tất cả sản phẩm là x - 2 (ngày)
Tổng số sản phẩm dự định làm được là: 30x (sản phẩm)
Tổng số sản phẩm thực tế làm được là: 33(x - 2) (sản phẩm)
Theo bài ra, ta có pt: 33(x - 2) - 30x = 15
<=> 33x - 66 - 30x = 15
<=> 3x = 15 + 66
<=> 3x = 81
<=> x = 27 (thỏa mãn)
Vậy số lượng sản phẩm mà tổ phải làm theo kế hoạch là 27 . 30 = 810 (sản phẩm)
Thực tế tổ sản xuất làm được số sản phẩm mỗi ngày là: 30 + (30 : 100 x 10) = 33 (sản phẩm)
Gọi số ngày dự định hoàn thành xong tất cả sản phẩm là x (ngày, x > 2)
Số ngày thực tế hoàn thành xong tất cả sản phẩm là x - 2 (ngày)
Tổng số sản phẩm dự định làm được là: 30x (sản phẩm)
Tổng số sản phẩm thực tế làm được là: 33(x - 2) (sản phẩm)
Theo bài ra, ta có pt: 33(x - 2) - 30x = 15
<=> 33x - 66 - 30x = 15
<=> 3x = 15 + 66
<=> 3x = 81
<=> x = 27 (thỏa mãn)
Vậy số lượng sản phẩm mà tổ phải làm theo kế hoạch là 27 . 30 = 810 (sản phẩm)
Gọi số sản phẩm phải làm theo qui định trong 1 ngày là x (sản phẩm) (0< x < 600)
số sản phẩm làm được khi tăng năng suất là y (sản phẩm) (y>0)
có : y = x + 10 (1)
Thời gian hoàn thành theo qui định là : \(\dfrac{600}{x}\) (ngày)
Thời gian làm 400 sp đầu là \(\dfrac{400}{x}\) (ngày)
Thời gian làm 200 sp còn lại là \(\dfrac{200}{y}\) (ngày)
Ta có: \(\dfrac{400}{x}\) + \(\dfrac{200}{y}\) = \(\dfrac{600}{x}\) - 1(2)
Thế (1) vào (2) ta có: \(\dfrac{400}{x}\) + \(\dfrac{200}{(x+10)}\) = \(\dfrac{600}{x}\) -1 ( ĐK : x > 0 )
=> 400.(x + 10) + 200.x = 600.(x + 10) - x.(x + 10 )
<=> 400x + 4000 + 200x = 600x + 6000 -\((x)^{2}\) - 10x
<=> \((x)^{2}\) + 10x - 2000 = 0
<=> \(\begin{cases} x = 40 (thỏa mãn) \\ x = - 50 (loại) \end{cases}\)
Vậy theo qui định mỗi ngày phải làm 40 sản phẩm.