Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
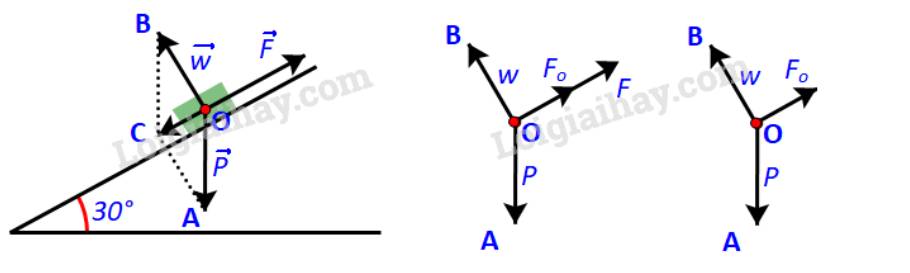
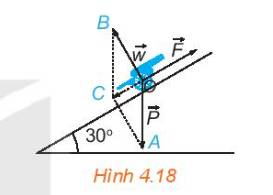
Khẩu pháo chịu tác động của ba lực: trọng lực \(\overrightarrow P \)(kí hiệu \(\overrightarrow {OA} \)), phản lực \(\overrightarrow w \)(kí hiệu \(\overrightarrow {OB} \)) và lực kéo \(\overrightarrow F \). Để kéo pháo thì độ lớn của lực kéo phải lớn hơn độ lớn của lực kéo khi pháo cân bằng \(\overrightarrow {{F_o}} \)(kí hiệu \(\overrightarrow {O{F_o}} \) )
Khi pháo cân bằng thì: \(\overrightarrow P + \overrightarrow w + \overrightarrow {{F_o}} = \overrightarrow 0 \)
Để tổng hợp lực \(\overrightarrow P \) và \(\overrightarrow w \), ta vẽ hình bình hành OACB.
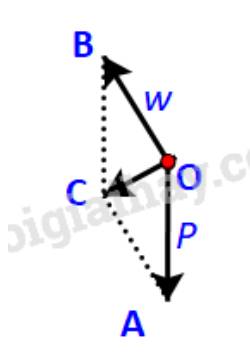
Ta có:
\(OB = \;AC;\;\;OB//\;AC\;\; \Rightarrow \overrightarrow {OB} = \;\overrightarrow {AC} \)
\( \Rightarrow \overrightarrow {OB} + \overrightarrow {OA} = \overrightarrow {AC} + \overrightarrow {OA} = \overrightarrow {OA} + \overrightarrow {AC} = \overrightarrow {OC} \)
\( \Rightarrow \overrightarrow 0 = \overrightarrow P + \overrightarrow w + \overrightarrow {{F_o}} = \overrightarrow {OB} + \overrightarrow {OA} + \overrightarrow {O{F_o}} = \overrightarrow {OC} + \overrightarrow {O{F_o}} \)
\( \Rightarrow \;O\) là trung điểm của \(C{F_o}\), hay \(OC = \left| {\overrightarrow {{F_o}} } \right|\).
Lại có: \(OB \bot \;\;OC\)(do \(\overrightarrow {OB} \) là phản lực)
\( \Rightarrow \;AC \bot CO \Rightarrow OC = OA\,.\,\,\cos \widehat {AOC}\)
Mà \(\widehat {AOC} = {90^o} - {30^o} = {60^o}\); \(\left| {\overrightarrow P } \right| = OA = 22\;148\;N\)
\( \Rightarrow OC = 22\;148\,.\,\,\cos {60^o} = 11074\;\left( N \right)\)
Vậy lực \(\overrightarrow {{F_o}} \)có độ lớn là \(11\;074\;N\), để kéo pháo thì lực \(\overrightarrow F \) cùng hướng với \(\overrightarrow {{F_o}} \) và \(\left| {\overrightarrow F } \right| > 11\;074\;N\)
Vì \(11\;074\;:100 = 110,74\) nên cần tối thiểu 111 người để kéo pháo.

a: Số cách chọn là: \(C^3_{25}=2300\left(cách\right)\)
b: Số cách chọn là: \(C^1_{15}\cdot C^2_{24}=4140\left(cách\right)\)

Chọn B.
Áp dụng định lí cosin trong tam giác ta có:
AB2 = AC2 + BC2 - 2BC.AC.cosC
= 2502 + 1202 - 2.250.120.cos78024’ = 64835
Suy ra AB = 255.