Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác ABC vuông tại B nên ta có: \(\tan C = \frac{{AB}}{{CB}} \Leftrightarrow AB = \tan {32^ \circ }.(1 + x)\)
Tam giác ADB vuông tại B nên ta có: \(\tan D = \frac{{AB}}{{DB}} \Leftrightarrow AB = \tan {40^ \circ }.x\)
\(\begin{array}{l} \Rightarrow \tan {32^ \circ }.(1 + x) = \tan {40^ \circ }.x\\ \Leftrightarrow x.(\tan {40^ \circ } - \tan {32^ \circ }) = \tan {32^ \circ }\\ \Leftrightarrow x = \frac{{\tan {{32}^ \circ }}}{{\tan {{40}^ \circ } - \tan {{32}^ \circ }}}\\ \Leftrightarrow x \approx 2,9\;(km)\end{array}\)
\( \Rightarrow AB \approx \tan {40^ \circ }.2,92 \approx 2,45\;(km)\)
Vậy chiều cao của ngọn núi là 2,45 km.

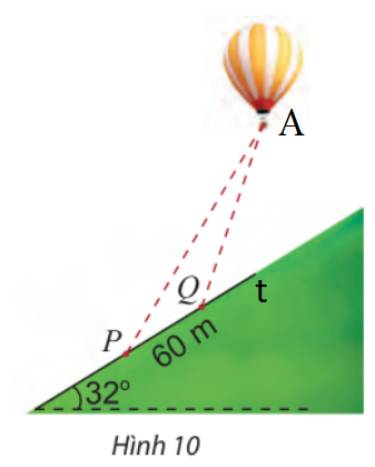
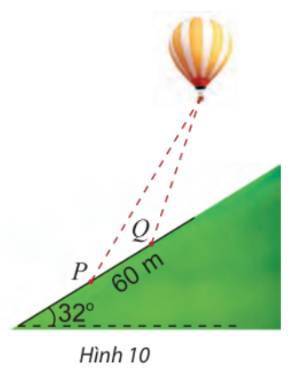
Gọi A là vị trí của khinh khí cầu, Pt là đường sườn đồi như hình.
Ta có:
Tại P, góc nâng của khinh khí cầu là \({62^ \circ }\)\( \Rightarrow \widehat P = {62^ \circ } - {32^ \circ } = {30^ \circ }\)
Tại Q, góc nâng của khinh khí cầu là \({70^ \circ }\)\( \Rightarrow \widehat {AQt} = {70^ \circ } - {32^ \circ } = {38^ \circ }\)
\( \Rightarrow \widehat {AQP} = {180^ \circ } - {38^ \circ } = {142^ \circ }\) và \(\widehat A = {180^ \circ } - {142^ \circ } - {30^ \circ } = {8^ \circ }\)
Áp dụng định lí sin trong tam giác APQ, ta có:
\(\begin{array}{l}\frac{{PQ}}{{\sin A}} = \frac{{QA}}{{\sin P}}\\ \Rightarrow QA = \sin P.\frac{{PQ}}{{\sin A}} = \sin {30^ \circ }.\frac{{60}}{{\sin {8^ \circ }}} \approx 215,56\;(m)\end{array}\)
Vậy khoảng cách từ Q đến khinh khí cầu là 215,56 m.

Gắn hệ trục Oxy vào chiếc cổng, gọi chiều cao của cổng là h ta vẽ lại parabol như dưới đây:
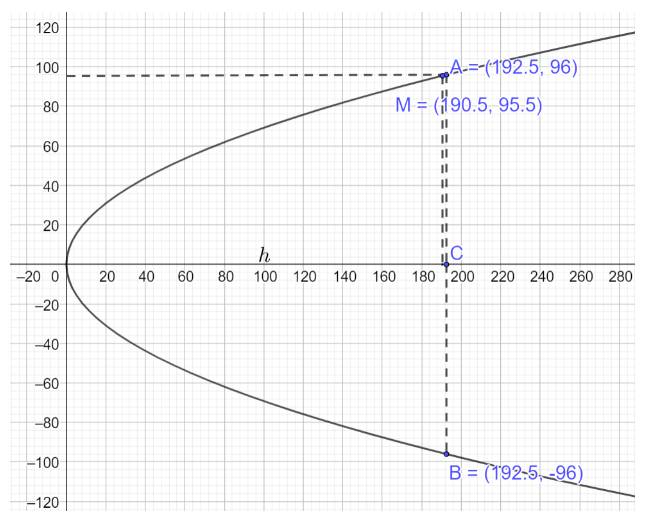
Phương trình parabol mô phỏng cổng có dạng \({y^2} = 2px\)
Theo giả thiết \(AB = 2{y_A} = 192 \Rightarrow {y_A} = 96,OC = h \Rightarrow M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\)
Thay tọa độ các điểm \(M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\) vào phương trình \({y^2} = 2px\) ta có:
\(\left\{ \begin{array}{l}95,{5^2} = 2p\left( {h - 2} \right)\\{96^2} = 2ph\end{array} \right. \Rightarrow \left\{ \begin{array}{l}p = \frac{{383}}{{16}}\\h \simeq 192,5\end{array} \right.\)
Vậy chiều cao của cổng gần bằng 192,5 m

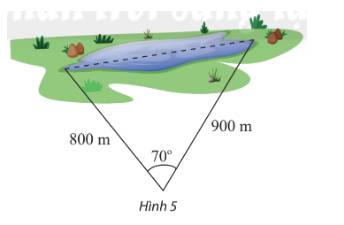
Kí hiệu hai vị trí đầu hồ và vị trí quan sát lần lượt bở các điểm A, B, C như hình dưới:
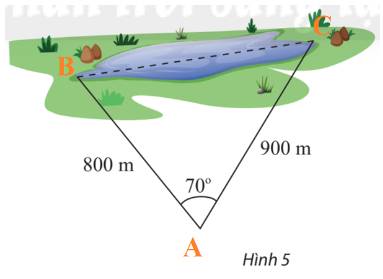
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\)
Mà \(AB = 800,AC = 900,\widehat A = {70^o}\)
\(\begin{array}{l} \Rightarrow B{C^2} = {900^2} + {800^2} - 2.900.800\cos {70^o} \approx 957490,9936\\ \Leftrightarrow BC \approx 978,5147\end{array}\)
Vậy khoảng cách giữa hai điểm ở hai đầu hồ là 978,5147 m.

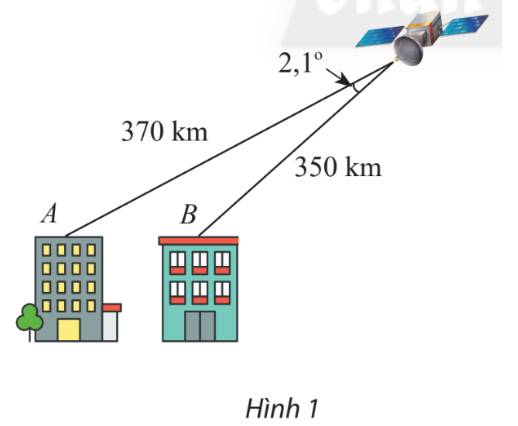
Áp dụng định lí cosin, ta có:
\(\begin{array}{l}A{B^2} = {370^2} + {350^2} - 2.370.350.\cos 2,{1^ \circ }\\ \Rightarrow AB \approx 23,96\;(km)\end{array}\)
Vậy khoảng cách giữa hai tòa nhà là 23,96 km.
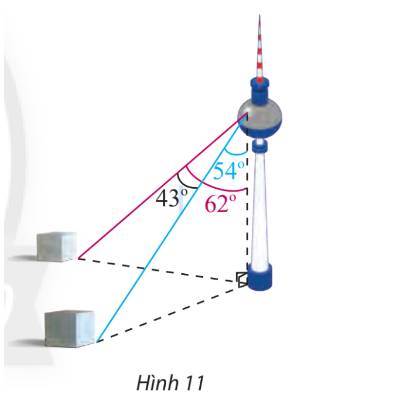



Gọi các điểm A, B, C, H như hình trên.
Xét tam giác ABH ta có:
\(AH = 352,\;\widehat {BAH} = {62^ \circ }\)
Mà \(\cos \widehat {BAH} = \frac{{AH}}{{AB}} \Rightarrow AB = 352 : \cos {62^ \circ } \approx 749,78\)
Tương tự, ta có: \(\cos \widehat {CAH} = \frac{{AH}}{{AC}} \Rightarrow AC = 352:\cos {54^ \circ } \approx 598,86\)
Áp dụng định lí cosin cho tam giác ABC, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\ \Leftrightarrow B{C^2} = {749,78^2} + {598,86^2} - 2.749,78.598,86.\cos {43^ \circ }\\ \Rightarrow BC \approx 513,84\end{array}\)
Vậy khoảng cách giữa hai cột mốc này là 513,84 m.