Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Chọn hệ quy chiếu Oxy như hình vẽ, chiều dương là chiều chuyển động. Vật chịu tác dụng của các lực f m s → ; N → ; P →
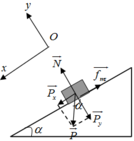
Theo định luật II newton ta có: f → m s + N → + P → = m a → 1
Chiếu Ox ta có :
P x − f m s = m a 1 ⇒ P sin α − μ N = m a 1
Chiếu Oy ta có: N = P y = P cos α
⇒ a 1 = g sin α − μ g cos α
⇒ a 1 = 10. 1 2 − 0 , 1.10. 3 2 = 4 , 134 m / s 2
Vận tốc của vật ở chân dốc.
Áp dụng công thức v 1 2 − v 0 2 = 2 a 1 s
⇒ v 1 = 2 a 1 s = 2.4 , 134.40 ≈ 18 , 6 m / s
b. Chọn hệ quy chiếu Oxy như hình vẽ , chiều dương (+) Ox là chiều chuyển động .Áp dụng định luật II Newton
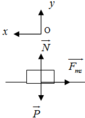
Ta có F → m s + N → + P → = m a → 2
Chiếu lên trục Ox: − F m s = m a 2 ⇒ − μ . N = m a 2 1
Chiếu lên trục Oy: N – P = 0 ⇒ N = P=mg
⇒ a 2 = − μ g = − 0 , 2.10 = − 2 m / s 2
Để vật dừng lại thì v 2 = 0 m / s
Áp dụng công thức:
v 2 2 − v 1 2 = 2 a 2 . s 2 ⇒ s 2 = − 18 , 6 2 2. − 2 = 86 , 5 m

Chọn đáp án B
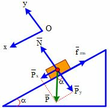
Chọn hệ quy chiếu Oxy như hình vẽ, chiều dương là chiều chuyển động. Vật chịu tác dụng của các lực ![]()
Theo định luật II newton ta có: ![]()
Chiếu Ox ta có
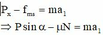
Chiếu Oy ta có:
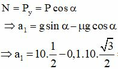
![]()
Vận tốc của vật ở chân dốc. Áp dụng công thức ![]()
![]() m/s
m/s

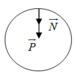
Người diễn viên chịu tác dụng của hai lực P → , N →
Theo định luật II Newton P → + N → = m a →
a. Chiếu theo chiều hướng vào tâm
P + N = m a h t = m . v 2 R ⇒ N = m . v 2 R − P
Muốn không bị rơi thì người đó vẫn ép lên vòng xiếc tức là
N ≥ 0 ⇒ m v 2 R − m g ≥ 0 ⇒ v ≥ g R ⇒ v ≥ 10.10 = 10 ( m / s )
Vậy vận tốc của xe đạp tối thiểu phải là 10m/s.
b. Chiếu theo chiều hướng vào tâm P cos α + N = m v 2 r
⇒ N = m v 2 r − g cos α = 60 10 2 10 − 10. cos 60 0 = 300 N

Để tính gia tốc và vận tốc của vật đối với lực ma sát, ta sử dụng công thức sau:
Gia tốc = F / m Vận tốc = gia tốc * t
Trong đó, F là lực tác động trên vật, m là khối lượng của vật, g là trường lực trọng dưới định luật của Newton, và t là thời gian.
Để tính quãng đường, ta sử dụng công thức:
quãng đường = 1/2 * m * vận tốc^2 / g
Lúc này, ta đã tính được gia tốc, vận tốc, và quãng đường của vật đi được sau khi tác dụng lực 5s.

a. Vì Xe chuyển động thẳng đều nên
F = f m s = μ N = μ m g = 0 , 2.2000.10 = 4000 ( N )
b. v C = 72 ( k m / h ) = 20 ( m / s )
Áp dụng định lý động năng
A = W d C − W d B
Công của trọng lực
A P = P x . B C = P sin α . B C = m g sin α . B C A P = 2000.10. 1 2 . B C = 10 4 . B C ( J )
⇒ 10 4 . B C = 1 2 . m . v C 2 − 1 2 m . v B 2 ⇒ 10 4 . B C = 1 2 .2000.20 2 − 1 2 .2000.2 2 ⇒ B C = 39 , 6 ( m )
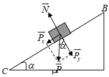
c. Áp dụng định lý động năng
A = W d D − W d C ⇒ A f → m s = 1 2 m v D 2 − 1 2 m v C 2
Công của lực ma sát
A f m s = − f m s . s = − μ N . s = − μ . m g . s / = − μ .2000.10.200 = − μ .4.10 6 ( J )
Dừng lại
v D = 0 ( m / s ) ⇒ − μ 4.10 6 = 0 − 1 2 .2000.20 2 ⇒ μ = 0 , 1

Chọn đáp án D
72 km/h = 20 m/s.
Xe chuyển động tròn đều nên ![]() đóng vai trò là lực hướng tâm.
đóng vai trò là lực hướng tâm.
Để xe không trượt trên đường thì:
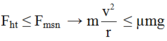
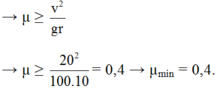

\(\left\{{}\begin{matrix}Ox:mg\sin\alpha-F_{ms}=m.a\\Oy:N=mg\cos\alpha\end{matrix}\right.\Rightarrow mg\sin\alpha-\mu mg\cos\alpha=ma\)
\(\Rightarrow a=g\sin\alpha-\mu g\cos\alpha=...\left(m/s^2\right)\)

Chọn D.
v = 72 km/h = 20 m/s.
Xe chuyển động tròn đều nên F m s n → đóng vai trò là lực hướng tâm.
Để xe không trượt trên đường thì
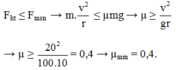

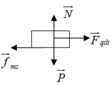
Để Ô tô không bị trượt khỏi đoạn đường đèo thì: F q t l t ≤ F m s
⇒ m v 2 r ≤ μ . N = μ . m . g
⇒ v ≤ r . μ . g = 2.0 , 8.10 = 4 m / s
⇒ v = r ω ≤ 4 ⇒ ω ≤ 4 2 = 2 r a d / s
Khi vào khúc quanh người và xe nghiêng về phía tâm khúc quanh.
Người và xe chịu tác dụng của trọng lực \(\overrightarrow{P}\), phản lực đàn hồi của mặt đường \(\overrightarrow{N}\) và lực ma sát \(\overrightarrow{F_{ms}}\). ( Hợp lực \(\overrightarrow{N}\) và \(\overrightarrow{F_{ms}}\) là phản lực tổng cộng \(\overrightarrow{Q}\) của mặt đường do xe nghiêng).
Theo định luật II Niu tơn hình vẽ:
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m\overrightarrow{a}\left(1\right)\)
Chiếu phương trình (1) lên trục thẳng đứng ta có:
\(-P+N=0\rightarrow N=P\left(2\right)\)
Chiếu phương trình (1) lên trục nằm ngang ( hướng tâm) ta có:
\(F_{ms}=m\frac{v^2}{R}\left(3\right)\)
Để xe khỏi trượt lực ma sát là lực ma sát nghỉ:
\(F_{_{ }ms}\le kN=kP=kmg\left(4\right)\)
Từ (3) và (4) ta suy ra:
\(v^2\le kgR\) hay \(v\le\sqrt{kgR}=4m\text{/}s\)
Góc nghiêng \(\alpha\) của xe khi \(v=10,8m\text{/}h=3m\text{/}s\) được xác định từ hệ thức:
\(\tan\alpha\frac{F_{ms}}{P}=\frac{v^2}{gR}\approx0,06\)
Vậy \(\alpha\approx\text{arctan 0,06}\)\(\approx3^o46'\)