Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
I ' I = k R 2 + Z C 2 R 2 + Z C k 2 ⇒ 3 2 1 = 3 · R 2 + Z C 2 R 2 + Z C 3 2 ⇒ Z C = 3 R 7

Chọn đáp án B
I ' I = k R 2 + Z L 2 R 2 + k Z L 2 ⇒ 3 1 = 3 · R 2 + Z L 2 R 2 + 3 Z L 2 ⇒ Z L = R 3

Chuẩn hóa R = 1
Gọi x là cảm kháng của cuộn dây khi roto quay với tốc độ n vòng/phút
Ta có I 1 I 2 = U 1 Z 2 U 2 Z 1 = 1 2 + 3 x 2 3 1 2 + x 2 = 1 3 ⇒ x = 1 3
→ Vậy khi roto quay với tốc độ 2n vòng/phút thì cảm kháng của đoạn mạch là
Đáp án B

Chọn A

Khi roto quay với tốc độ n vòng/phút :
I= 3 = U R 2 + Z C 1 2 = k n R 2 + Z C 1 2
Khi roto quay với tốc độ 3n vòng/phút:
I=9= U R 2 + Z C 2 2 = 3 k n R 2 + Z C 1 2 9
Lấy(1) chia (2):
3 9 = 1 3 R 2 + Z C 1 2 9 R 2 + Z C 1 2 => ZC1 = R 3 ; ZC2 = R 3 3 = Z C 1 3
Khi roto quay với tốc độ 2n vòng/phút :
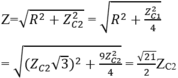

Chọn đáp án C
Lúc đầu:
Z C = R , Z L = R 4 ⇒ I ' I = k R 2 + Z L - Z C 2 R 2 + k Z L - Z C k 2 = 2 R 2 + R 4 - R 2 R 2 + 2 R 4 - R 2 2 = 2 , 5

Chọn đáp án B
tan φ = Z L - Z C R = tan π 3 ⇒ Z L - Z C = R 3 I ' I = k R 2 + Z L - Z C 2 R 2 + k Z L - Z C k 2 = 2 R 2 + ( R 3 ) 2 R 2 + 2 Z L - Z C 2 2 = 8 ⇒ I ' = 8 ( A )

Đáp án: C
f = n 1 p = 25 H z ⇒ ω = 2 πf = 50 π Z L = ω L = 100 Ω ; Z C = 1 ω C = 200 Ω E = N 2 πfΦ 0 2 ⇒ I 1 = E 1 R 2 + Z L - Z C 2 ⇒ E 1 = 200 V
Đặt n = xn1
⇒ I = x E R 2 + x Z L - Z C x 2
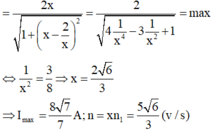

Chọn đáp án B
I 1 = E 1 R 2 + Z 4 2 = 1 ; I 2 = 2 E 1 R 2 + 4 Z L 1 2 = 0 , 4 2 ⇒ Z 4 = R E 1 = R 2 I 3 = 3 E 1 R 2 + 9 Z L 1 2 = 3 R 2 R 2 + 9 R 2 = 3 0 , 2 ( A )

Với n = n1 , ta có ZC1 = R = 1 (ta chuẩn hóa R=1 )
- Khi n = n2 = 4.n1/3 ⇒ ZC2 = 3/4 , điện áp hiệu dụng trên tụ cực đại:
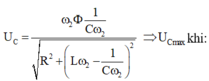
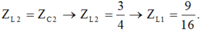
- Khi n = n3 (giả sử gấp a lần n1 ), cường độ dòng điện hiệu dụng trong mạch là cực đại:
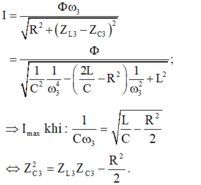
- Thay kết quả cuân hóa vào phương trình trên, ta được:
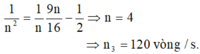
\(n=n_1=\dfrac{60v}{s} \Rightarrow R=Z_{C_1} \Rightarrow \omega _1.R.C=1 \)
\(n=n_2: U_C=\dfrac{\dfrac{\Phi}{\sqrt2}.\omega .\dfrac{1}{\omega .C}}{\sqrt{\left(Z_L-Z_C\right)^2+R^2}}=\dfrac{\dfrac{\Phi}{\sqrt2}.\dfrac{1}{C} }{\sqrt{\left(Z_L-Z_C\right)^2+R^2}} \)
\(U_{C_{max}} \Leftrightarrow Z_L=Z_C\rightarrow LC=\dfrac{1}{\omega _2^2} \)
\(I=\dfrac{\dfrac{\Phi}{\sqrt2}.\omega }{\sqrt{\left(Z_L-Z_C\right)^2+R^2}} \)
\(n=n_3 \) Thay đổi \(\omega \) để I max trong trường hợp này tương tự thay đổi \(\omega\) để \(U_L\) max trong mạch RCL nối tiếp
\(\rightarrow \dfrac{1}{\omega _3.C} =\sqrt{\dfrac{L}{C}-\dfrac{R^2}{2}} \rightarrow \omega _3=\dfrac{1}{C.\sqrt{\dfrac{L}{C}-\dfrac{R^2}{2} }}=\dfrac{1}{\sqrt{LC-\dfrac{R^2C^2}{2}}}\)
\(=\dfrac{1}{\sqrt{\dfrac{1}{\omega _2^2}-\dfrac{\left(\dfrac{1}{\omega _1^2}\right) }{2} } } \)
Vậy:\(n_3=\dfrac{1}{\sqrt{\dfrac{1}{n_2^2}-\dfrac{1}{2.n_1^2} }}=240 \dfrac{v}{s}\)
ad cho em hỏi sao Uc max lại là cộng hưởng U I max giống UL max em tưởng UC max với UL max có Ct tính gần giống nhau chứ