Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gia tốc của vật : a = F/m = 5/10 = 0,5(m/ s 2 )
Quãng đường vật dịch chuyển: s = a t 2 /2 = 0,5 t 2 /2 = 0,25 t 2
Công của lực thực hiện: A = Fs.
- Trong giây thứ nhất (từ 0 đến 1s):
s 1 = 0,25 t 1 2 = 0,25( 1 2 - 0) = 0,25(m)
Suy ra: A 1 = F s 1 = 5.0,25 = 1,25 J.
- Trong giây thứ 2 (từ 1s đến 2s):
s 2 = 0,25( t 2 2 - t 1 2 ) = 0,25( 2 2 - 1 2 ) = 0,75(m)
Suy ra: A 2 = F s 2 = 5.0,75 = 3,75 J.
Trong giây thứ ba (từ 2s đến 3s):
s 3 = 0,25( t 3 2 - t 2 2 ) = 0,25( 3 2 - 2 2 ) = 1,25(m)
Suy ra: A 3 = F s 3 = 5.1,25 = 6,25 J.
Vận tốc của vật ở cuối giây thứ ba: v = v0 + at = 0 + 2,5.3 = 7,5 m/s.
\(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\Rightarrow F=m.a\Leftrightarrow a=\frac{5}{10}=0,5\left(m/s^2\right)\)
Trong giây thứ nhất đi được:
\(S=\frac{1}{2}at^2=\frac{1}{2}.0,5.1=0,25\left(m\right)\)
\(\Rightarrow A_1=Fs.\cos\alpha=5.0,25=1,25\left(J\right)\)
Trong giây thứ hai đi được:
\(S_2=\frac{1}{2}at_2^2-\frac{1}{2}at^2_1=\frac{1}{2}.0,5\left(4-1\right)=0,75\left(m\right)\)
\(\Rightarrow A_2=5.0,75=3,75\left(J\right)\)
Tương tự với giây thứ 3
a)Độ lớn lực ma sát:
\(F_{ms}=\mu mg=0,02\cdot10\cdot10=2N\)
Công lực ma sát: \(A_{ms}=F_{ms}\cdot s=2\cdot5=10m\)
b)Bảo toàn động năng:
\(A_F=\Delta W=\dfrac{1}{2}m\left(v_2^2-v_1^2\right)=\dfrac{1}{2}\cdot10\cdot\left(5^2-0^2\right)=125J\)
\(\Rightarrow F_k=\dfrac{A_F}{s}=\dfrac{125}{5}=25N\)
a) (3 điểm)
Các lực tác dụng lên vật được biểu diễn như hình vẽ. (1,00đ)
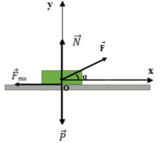
Chọn hệ trục Ox theo hướng chuyển động, Oy vuông góc phương chuyển động.
*Áp dụng định luật II Niu – tơn ta được:
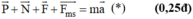
Chiếu hệ thức (*) lên trục Ox ta được: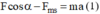 
(0,50đ)
Chiếu hệ thức (*) lên trục Oy ta được:
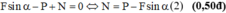
Mặt khác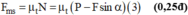 
Từ (1), (2) và (3) suy ra:
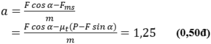
b) (1 điểm)
Quãng đường mà vật đi được trong giây thứ 5 là:
S = S 5 – S 4 = 0,5.a. t 5 2 – 0,5.a. t 4 2 = 0,5.1,25. 5 2 - 0,5.1,25. 4 2 = 5,625 m. (1,00đ)
a) Dựng hệ trục tọa độ Oxy như hình vẽ. Chọn chiều (+) là chiều chuyển động của vật. Ta chiếu \(\overrightarrow{F_k}\) thành 2 lực \(\overrightarrow{F_{k_x}},\overrightarrow{F_{k_y}}\). Khi đó \(F_{k_x}=F_k.\cos60^o=24\left(N\right)\) và \(F_{k_y}=F_k.\sin60^o=24\sqrt{3}\left(N\right)\)
Áp dụng định luật II Newton, ta có: \(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_k}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}=5.\overrightarrow{a}\) (*)
Chiếu (*) lên Oy, ta được \(N=P-F_{k_y}=50-24\sqrt{3}\left(N\right)\)
Do đó \(F_{ms}=\mu.N=0,1\left(50-24\sqrt{3}\right)\approx0,843\left(N\right)\)
Chiếu (*) lên Ox, ta được:
\(F_{k_x}-F_{ms}=5.a\)
\(\Rightarrow48-0,843=5a\Leftrightarrow a=9,43\left(m/s^2\right)\)
b) Gọi \(v\) là giá trị vận tốc của vật sau khi vật đi được 16m. Do ban đầu vật đứng yên nên \(v_0=0\left(m/s\right)\). Ta có:
\(v^2-v_0^2=2as\Leftrightarrow v^2=2as=2.9,43.16=301,76\) \(\Rightarrow v\approx17,37\left(m/s\right)\)
c) Khi lực kéo dừng lại, thì chỉ còn lực ma sát trượt ảnh hưởng đến chuyển động của vật. Khi đó, gia tốc \(a'=\dfrac{-F_{ms}}{m}=-0,1686\left(m/s^2\right)\)
Như vậy, vật sẽ chuyển động chậm dần đều với gia tốc \(a'\approx-0,1686\left(m/s^2\right)\)
hợp với hướng chuyển động một góc α = 30° (Hình vẽ). Hệ số ma sát trượt giữa vật và sàn là μt = 0,30. Cho biết độ lớn lực kéo F = 17N và gia tốc trọng trường g = 10m/
s
2