Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
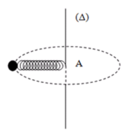
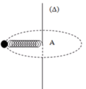
Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm.
Khi trục Δ quay thì lò xo giãn ra một đoạn ∆ℓ.
Fht = Fdh ↔ mω2(ℓo + ∆ℓ) = k.∆ℓ → (k – mω2).∆ℓ = mω2ℓo


Đáp án A
Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm.
Khi trục Δ quay thì lò xo giãn ra một đoạn Δ l
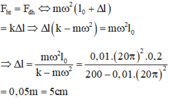

Chọn A
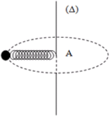
Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm.
Khi trục quay thì lò xo giãn ra một đoạn Δl
F h t = F d h ↔ m ω 2 ( l 0 + Δℓ) = k.Δℓ → (k – m ω 2 ).Δℓ = m ω 2 l 0
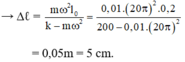

Ta có: ω = 2 π f = 2 π 360 60 = 12 π
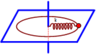
Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm:
Khi trục Δ quay thì lò xo dãn một đoạn Δl
→ F h t = F d h ↔ m ω 2 ( l 0 + Δ l ) = k Δ l → Δ l ( k − m ω 2 ) = m ω 2 l 0 → Δ l = m ω 2 l 0 k − m ω 2 = 0 , 01. ( 12 π ) 2 0 , 4 125 − 0 , 01. ( 12 π ) 2 = 0 , 0513 m = 5 , 13 c m
Đáp án: C

a.Ta có ω = 2 π f = 2 π .2 = 4 π r a d / s
Khi vật quay tròn đều F d h = F q t l t ⇒ k . Δ l = m . r . ω 2
Mà r = l 0 + Δ l ⇒ k . Δ l = m . l 0 + Δ l . ω 2 ⇒ 12 , 5. Δ l = 0 , 01. 0 , 2 + Δ l . 4 π 2
⇒ Δ l = 0 , 03 m = 3 c m
b. Theo bài ra r max = l max = 0 , 4 m
⇒ F d h ≥ F q t l t ⇒ k . Δ l ≥ m . r . ω 2 ⇒ ω ≤ k . Δ l m . r
Mà Δ l = l 1 − l 0 = 40 − 20 = 20 c m = 0 , 2 m
⇒ ω ≤ 12 , 5.0 , 2 0 , 01.0 , 4 = 25 r a d / s Vậy n = 25.60 2. π = 238 , 73 ( vòng/ phút )

Đáp án A
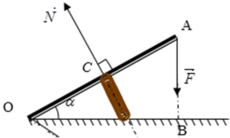
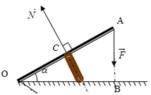
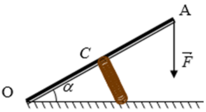
Ta vận dụng quy tắc mô men lực để tìm N.
Điều kiện cân bằng của thanh OA quanh trục O là:
MF = MN ↔ F.OB = N.OC với OB = 2OC.cosα
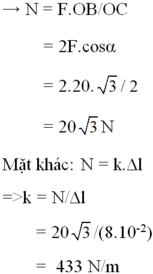

Chọn A.
Ta vận dụng quy tắc mô men lực để tìm N.
Điều kiện cân bằng của thanh OA quanh trục O là:
MF = MN
↔ F.OB = N.OC với OB = 2OC.cosα
→ N = F.OB/OC = 2F.cosα
= 2.20. 3 /2 = 20 3 N
Mặt khác: N = k.Δl => k = N/Δl = 20 3 /(8.10-2) = 433 N/m

Chọn A.
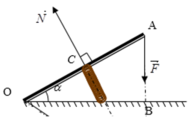
Ta vận dụng quy tắc mô men lực để tìm N.
Điều kiện cân bằng của thanh OA quanh trục O là:
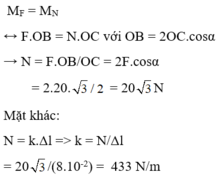



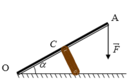
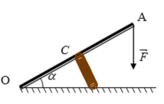
Chọn đáp án A
Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm.
Khi trục ∆ quay thì lò xo giãn ra một đoạn ∆ℓ.
Fht = Fdh
<-> mω2(ℓo + ∆ℓ) = k.∆ℓ
→ (k – mω2).∆l = mω2ℓo