Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Tại vị trí lò xo nén 10cm, cơ năng dàn hồi của vật bằng:
1 2 m v 2 + 1 2 k Δ l 2 = 1 2 500 0 , 1 2 = 2 , 5 J
Cơ năng đó có giá trị bằng động năng tại vị trí cân bằng
( thế năng bằng 0 ở vị trí cân bằng )


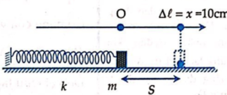

+ Khi tính công ta chú ý rằng không tính công của lực đàn hồi. Do vậy ta có:
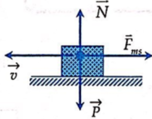
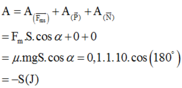
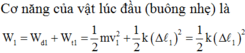
Cơ năng của vật sau khi tắt hẳn (dừng lại) là
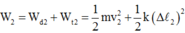
![]()
Do vật chịu tác dụng thêm lực ma sát cơ năng của vật sẽ biến đổi. Công của các lực cản bằng độ biến thiên cơ năng của vật:
![]()
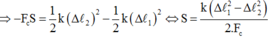
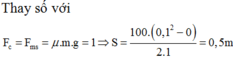


+ Khi tính công ta chú ý rằng không tính công của lực đàn hồi. Do vậy ta có:
![]()
![]()
Cơ năng của vật lúc đầu (buông nhẹ) là
![]()
Cơ năng của vật sau khi tắt hẳn (dừng lại) là
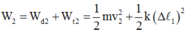
![]()
Do vật chịu tác dụng thêm lực ma sát cơ năng của vật sẽ biến đổi. Công của các lực cản bằng độ biến thiên cơ năng của vật:
![]()
![]()
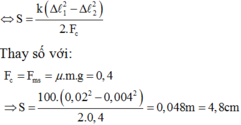

Thế năng đàn hồi:
\(W_{đh}=\dfrac{1}{2}k\cdot\left(\Delta x\right)^2=\dfrac{1}{2}\cdot250\cdot0,04^2=0,2J\)
Thế năng đàn hồi không phụ thuộc vào khối lượng vật.




Ở vị trí ban đầu lò xo bị kéo dãn một đoạn nên cơ năng hệ:
\(W_0=\dfrac{1}{2}k\cdot\left(\Delta l\right)^2\)
Tại vị trí cân bằng lò xo không biến dạng nên cơ năng hệ:
\(W=\dfrac{1}{2}mv^2\)
Bảo toàn cơ năng cho chuyển động của hệ:
\(W=W_0=\dfrac{1}{2}k\cdot\left(\Delta l\right)^2=\dfrac{1}{2}\cdot100\cdot\left(0,1\right)^2=0,5J\)
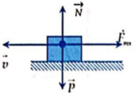
Hệ vật “Quả cầu – Lò xo – Trái Đất” là hệ cô lập, do không chịu tác dụng các ngoại lực (lực ma sát, lực cản), chỉ có các nội lực tương tác (trọng lực, phản lực, lực đàn hồi), nên cơ năng của hệ vật bảo toàn.
Chọn vị trí cân bằng của hệ vật làm gốc tính thế năng đàn hồi, chiều lò xo bị kéo dãn là chiều dương.
– Tại vị trí ban đầu : quả cầu có vận tốc v0 = 0 và lò xo bị kéo dãn một đoạn Δl0> 0 cm, nên cơ năng của hệ vật:
\({{\rm{W}}_0} = {{k{{\left( {\Delta {l_0}} \right)}^2}} \over 2}\)
– Tại vị trí cân bằng: quả cầu có vận tốc v ≠ 0 và lò xo không bị biến dạng (Δ= 0), nên cơ năng của hệ vật :
liệu có đúng