Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Áp dụng công thức lăng kính: S i n i 1 = n . sin r 1 S i n i 2 = n . sin r 2 r 1 + r 2 = A D = ( i 1 + i 2 ) − A
+ Đối với tia đỏ: s i n i 1 = n d . sin r 1 d ⇒ sin r 1 d = sin 60 0 n d ⇒ r 1 d = 34 , 22 0 r 1 d + r 2 d = A ⇒ r 2 d = A − r 1 d = 15 , 78 0 s i n i 2 d = n . sin r 2 d ⇒ sin r 2 d = n d sin r 2 d ⇒ i 2 d = 24 , 76 0 D = ( i 1 + i 2 d ) − A = 60 0 + 24 , 76 0 − 50 0 = 34 , 76 0
+ Đối với tia tím: s i n 60 0 = n t . sin r 1 t ⇒ r 1 t = 33 , 24 0 r 1 t + r 2 t = A ⇒ r 2 t = A − r 1 t = 16 , 76 0 s i n i 2 t = n . sin r 2 t ⇒ sin r 2 t = n t sin r 2 t ⇒ i 2 t = 27 , 1 0 D = i 1 + i 2 d − A = 60 0 + 27 , 1 0 − 50 0 = 37 , 1 0
+ Góc hợp bởi giữa hai tia đỏ và tia tím sau khi ló ra khỏi lăng kính: D t - D d = 2 , 34 °

Chọn đáp án C.
δ = ( n t − n d ) A = ( 1 , 68 − 1 , 62 ) 6 0 = 0 , 36 0 ⇔ 0 , 006 ( r a d ) .

Chọn đáp án C.
n sin A = sin i ⇒ n d sin A = sin i d ⇒ 1 , 532 sin 30 0 = sin i d ⇒ i d ≈ 50 0 n t sin A = sin i t ⇒ 1 , 5867 sin 30 0 = sin i t ⇒ i t ≈ 52 , 5 0
⇒ δ = i t − i d = 2 , 5 0 .

Đáp án C
+ Tia đỏ vừa vặn phản xạ toàn phần, thì ta có thể lập luận để thấy rằng toàn bộ các tia khác cũng bị phản xạ toàn phần trên AC và khi đến BC đều ló hết ra ngoài

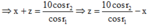
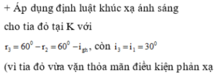
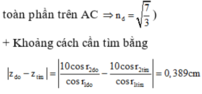

Đáp án B
+ Góc lệch qua lăng kính với trường hợp góc tới nhỏ D = A(n – 1) → ΔD = A(nt – nd) = 0,0044 rad.
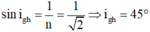
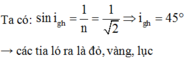
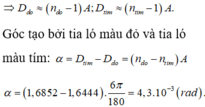
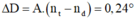
Tia đỏ có tia ló đối xứng qua mặt phân giác --> Tia đỏ có góc lệch cực tiểu, khi đó, bạn vẽ hình ra sẽ tìm được góc tới i1
sin i1 / sin 300 = căn 2 --> i1 = 450.
Sau đó, áp dụng công thức thấu kính để tìm góc r2, bạn sẽ thấy xảy ra phản xạ toàn phần với một phần tia sáng --> Tia màu tím không ló ra được
--> Đáp án A sai.