Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số \(T\left( t \right)\) có tập xác định là \(\left[ {0;100} \right]\).
Ta có: \(T\left( {60} \right) = 10 + 2.60 = 130\)
\(\begin{array}{l}\mathop {\lim }\limits_{t \to {{60}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ + }} \left( {k - 3t} \right) = k - 3.60 = k - 180\\\mathop {\lim }\limits_{t \to {{60}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ - }} \left( {10 + 2t} \right) = 10 + 2.60 = 130\end{array}\)
Để hàm số liên tục trên tập xác định thì hàm số phải liên tục tại điểm \({t_0} = 60\)
Khi đó: \(\mathop {\lim }\limits_{t \to {{60}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ - }} T\left( t \right) = T\left( {60} \right) \Leftrightarrow k - 180 = 130 \Leftrightarrow k = 310\)
Vậy với \(k = 310\) thì hàm số \(T\left( t \right)\) liên tục trên tập xác định.

a: Nhiệt độ ban đầu là:
\(T=25+70\cdot e^{-0.5\cdot0}=95\left(^0C\right)\)
b: ĐặtT=30
=>\(25+70\cdot e^{-0.5t}=30\)
=>\(e^{-0.5t}=\dfrac{1}{14}\)
=>\(-0.5t=ln\left(\dfrac{1}{14}\right)\)
=>\(t\simeq5,28\simeq6\)
=>Sau 6 phút thì nhiệt độ còn lại tầm 30 độ C

Ta có:
\(T'\left(t\right)=-0,1\cdot2t+1,2=-0,2t+1,2\)
Tốc độ thay đổi của nhiệt độ ở thời điểm t = 1,5s là:
\(T'\left(1,5\right)=-0,2\cdot1,5+1,2=0,9\)

\(\begin{array}{l} - 1 \le sin\frac{\pi }{{12}}(t - 9)\; \le 1\\ \Leftrightarrow - 3 \le 3sin\frac{\pi }{{12}}(t - 9)\; \le 3\\ \Leftrightarrow - 26 \le 29 + 3sin\frac{\pi }{{12}}(t - 9)\; \le 32\\ \Leftrightarrow - 26 \le h(t) \le 32\end{array}\)
Vâỵ nhiệt độ thấp nhất trong ngày là 26°C khi:
\(\begin{array}{l}29 + 3sin\frac{\pi }{{12}}(t - 9) = 26\\ \Leftrightarrow sin\frac{\pi }{{12}}(t - 9) = - 1\\ \Leftrightarrow \frac{\pi }{{12}}(t - 9) = - \frac{\pi }{2} + k2\pi \\ \Leftrightarrow t = 3 + 24k,k \in \mathbb{Z}.\end{array}\)
Do t là thời gian trong ngày tính bằng giờ nên \(0 \le t \le 24\). Suy ra: \(k = 0 \Rightarrow t = 3\).
Vì vậy vào thời điểm 3 giờ trong ngày thì nhiều độ thấp nhất của thành phố là 26°C.
Đáp án: C

a)Độ pH của nước cất là:
\(pH=-log\left[H^+\right]=-log\left[10^{-7}\right]=7\)
b)Độ pH của dung dịch đó là:
\(pH=-log\left[H^+\right]=-log\left[20.10^{-7}\right]\approx5,7\)

Đổi \(200km/h = \frac{{500}}{9}m/s\)
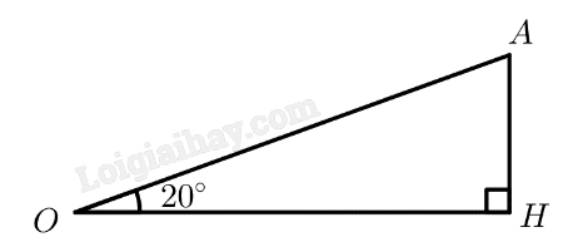
Mô hình hoá như hình vẽ, với \(OA\) là quãng đường máy bay bay được sau 2 giây, \(OH\) là độ cao của máy bay so với mặt đấy khi máy bay bay được sau 2 giây, độ lớn của góc \(\widehat {AOH}\) chỉ số đo góc giữa máy bay với mặt đất.
Sau 2 giây máy bay bay được quãng đường là: \(\frac{{500}}{9}.2 = \frac{{1000}}{9}\left( m \right)\)
Vì tam giác \(OAH\) vuông tại \(H\) nên ta có:
\(AH = OA.\sin \widehat {AOH} = \frac{{1000}}{9}.\sin {20^ \circ } \approx 38,0\left( m \right)\)
Vậy độ cao của máy bay so với mặt đất là 38 mét sau khi máy bay rời khỏi mặt đất 2 giây.

a) Tại thời điểm t = 2 độ sâu của nước là: \(h\left( 2 \right) = 0,8cos0,5.2 + 4 \approx 4,43{\rm{ }}m.\)
Vậy độ sâu của nước ở thời điểm t = 2 là khoảng 4,43 m.
b) Các thời điểm để mực nước sâu là 3,6m tương ứng với phương trình \(0,8cos0,5t + 4 = 3,6\).
Ta có: \(0,8cos0,5t + 4 = 3,6\)
\(\begin{array}{l} \Leftrightarrow cos0,5t = - \frac{1}{2} = cos\frac{{2\pi }}{3}\\ \Leftrightarrow 0,5t = \pm \frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}\\ \Leftrightarrow t = \pm \frac{{4\pi }}{3} + k4\pi ,k \in \mathbb{Z}\end{array}\)
Với \(t = \frac{{4\pi }}{3} + k4\pi \), trong 12 tiếng ta có các thời điểm \(0 \le \frac{{4\pi }}{3} + k4\pi \le 12 \Leftrightarrow - 0,3 \le k \le 0,62 \Rightarrow k = 0. \Rightarrow t = \frac{{4\pi }}{3}\)
Với \(t = - \frac{{4\pi }}{3} + k4\pi \), trong 12 tiếng ta có các thời điểm \(0 \le - \frac{{4\pi }}{3} + k4\pi \le 12 \Leftrightarrow 0,3 \le k \le 1,28 \Rightarrow k = 1 \Rightarrow t = - \frac{{4\pi }}{3} + 4\pi = \frac{{8\pi }}{3}\)
Vậy tại các thời điểm \(t = \frac{{4\pi }}{3}\), \(t = \frac{{8\pi }}{3}\) giờ thì tàu có thể hạ thủy.


Gọi un là nhiệt độ của khay nước đó sau n giờ (đơn vị độ C) với n ∈ ℕ*.
Ta có: u1 = 23; u2 = 23 – 23.20% = 23.(1 – 20%) = 23.80%; u3 = 23.80%.80% = 23.(80%)2; ...
Suy ra dãy (u1) lập thành một cấp số nhân với số hạng đầu u1 = 23 và công bội q = 80% có số hạng tổng quát un = 23.(80%)n-1 oC.
Vậy sau 6 giờ thì nhiệt độ của khay là u6 = 23.(80%)5 ≈ 7,5°C.