Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu là số cách chọn ngẫu nhiên 5 viên bi từ hộp chứa 18 viên bi.Suy ra số phần tử của không gian mẫu là Ω = C 18 5 = 8568
Gọi A là biến cố "5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng". Ta có các trường hợp thuận lợi cho biến cố A là:

Chọn A

gọi \(\Omega\)" chọn đc 3 viên bi trong 12 viên bi"
\(\left|\Omega\right|=C^3_{12}\)
A"chọn đc 3 viên bi có đủ 3 màu"
\(\left|A\right|=C^1_3.C^1_4.C^1_5\)
\(P\left(A\right)=\frac{\left|A\right|}{\left|\Omega\right|}=\frac{C^1_3.C^1_4.C^1_5}{C^3_{12}}\)

Đáp án A
Lấy ngẫu nhiên 3 viên bi trong 12 viên bi có C 12 3 = 220 cách ⇒ n Ω = 220 .
Gọi X là biến cố “3 bi được chọn có đủ 3 màu”
Lấy 1 viên bi màu đỏ trong 3 bi đỏ có 3 cách.
Lấy 1 viên bi màu xanh trong 4 bi xanh có 4 cách.
Lấy 1 viên bi màu vàng trong 5 bi vàng có 5 cách.
Suy ra số kết quả thuận lợi cho biến cố X là n X = 3 . 4 . 5 = 60 . Vậy P = n X n Ω = 3 11 .

Chọn B
Chọn 4 viên bất kì trong 15 viên bi, số cách chọn là n(Ω)=1365 cách
Gọi A là biến cố “4 viên bi lấy ra không đủ cả ba màu”
Trường hợp 1: Chọn 2 đỏ, 1 trắng, 1 vàng có C 6 2 . C 5 1 . C 4 1 = 300 cách
Trường hợp 2: Chọn 1 đỏ, 2 trắng, 1 vàng có C 6 1 . C 5 2 . C 4 1 = 240 cách
Trường hợp 3: Chọn 1 đỏ, 1 trắng, 2 vàng có C 6 1 . C 5 1 . C 4 2 = 180 cách
Theo quy tắc cộng số cách chọn viên bi có đủ 3 màu là 300 + 240 + 180 = 720 cách
Từ đó suy ra số cách chọn 4 viên bi không đủ 3 màu là n ( A ) = 1365 - 720 = 645
Xác suất cần tìm là P ( A ) = 645 1365 = 43 91

Giả sử trong tình huống xấu nhất ta chọn ngẫu nhiên 13 viên bi mà chỉ có bi màu vàng và màu xanh. Do để được chắc chắn 2 viên bi màu đỏ ta cần chọn thêm 2 viên bi nữa. Vậy cần chọn ít nhất 15 viên bi để chắc chắn được ít nhất 2 viên bi màu đỏ. Chọn B





Số cách chọn viên bi bất kì trong hộp là: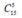 cách.
cách.
Khi chọn bất kỳ thì bao gồm các trường hợp sau
Suy ra số cách chọn thỏa mãn yêu cầu bài toán (có đủ ba màu) là
Chọn B.