Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi ∆ N 1 là số hạt β - được phóng ra trong khoảng thời gian ∆ t 1 kể từ thời điểm ban đầu.
Ta có
∆ N 1 = N 01 - N 1 = N 01 1 - e - k ∆ t 1
với N 01 là số hạt phóng xạ β - ban đầu.
Sau 3 giờ, số nguyên tử còn lại trong chất phóng xạ là N 02 = N 01 . e - 3 k .
Kể từ thời điểm này, trong khoảng thời gian ∆ t 2 thì số hạt β - tạo thành là
∆ N 2 = N 02 - N 01 = N 02 1 - e - k ∆ t 2
Cho ∆ t 1 = ∆ t 2 = 1 phút thì theo giả thiết, ta có ∆ N 1 = 960; ∆ N 2 = 120. Khi đó
∆ N 1 ∆ N 2 = e - 3 k ⇔ 120 960 = e - 3 k ⇔ 8 - 1 = e - 3 k ⇔ k = ln 2
Vậy T = k ln 2 = 1 (giờ) là chu kỳ bán rã của chất phóng xạ.
Đáp án B

Đáp án A.
Ta có:
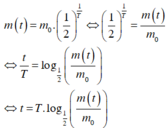
Theo giả thiết ta có:
T = 1602(năm), m 0 = 1 g r a m , m t = 0.5 g r a m
Áp dụng công thức ta có khoảng thời gian cần tìm là:
t = T . log 1 2 m t m 0 = 1602. log 1 2 0.5 1 = 1602. log 1 2 1 2 = 1602
Vậy sau 1602 năm thì 1gram chất phóng xạ này bị phân ra còn lại 0.5 gram

Đáp án A
Khi 2 chất điểm có vận tốc bằng nhau:
⇒ f ' t = g ' t = 1 − t = 4 cos t ⇒ t = A t = B A < 2 < B
Do đó quãng đường mà chất điểm A đã di chuyển là
S = ∫ A B 2 − t d t = ∫ A 2 2 − t d t + ∫ 2 B 2 − t d t = ∫ A 2 2 − t d t + ∫ 2 B t − 2 d t = 2 t − t 2 2 A 2 + t 2 2 − 2 t 2 B = 2 − 2 A + A 2 2 + B 2 2 − 2 B + 2 = 4 − 2 A + B + 1 2 A 2 + B 2 = 4 − 2 t 1 + t 2 + 1 2 t 1 2 + t 2 2

Đáp án A
Cách 1: Ta có f ' t = 2 − t ; g ' t = 4 cos t
Vẽ đồ thị hàm số y = f ' t và y = g ' t ta có
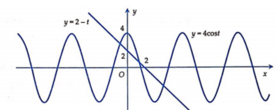
Nhìn vào đồ thị ta thấy 0 < t 1 < t 2 f ' t 1 > 0 f ' t 2 < 0 f 2 = 0 và f 2 = − 6 + 4 − 2 = − 4 f t 1 = − 6 + 2 t 1 − 1 2 t 1 2 f t 2 = − 6 + 2 t 2 − 1 2 t 2 2
⇒ s = f 2 − f t 1 + f 2 − f t 2 = − 4 − − 6 + 2 t 1 − 1 2 t 1 2 + − 4 − − 6 + 2 t 2 − 1 2 t 2 2
= 4 + 1 2 t 1 2 + t 2 2 − 2 t 1 + t 2
Sử dụng tích phân
Từ cách 1 ta có hai chất điểm gặp nhau khi 2 − t = 4 cos t ⇔ t 1 = A t 2 = B
Từ hình vẽ ở cách 1 ta có A < 2 < B
Quãng đường đi được từ thời điểm A đến thời điểm B được tính bằng công thức
∫ A B 2 − t d t = ∫ A 2 2 − t d t + ∫ 2 B 2 − t d t = ∫ A 2 2 − t d t + ∫ 2 B t − 2 d t
= 2 t − t 2 2 2 A + t 2 2 − 2 t B 2
= 4 − 2 − 2 A + A 2 2 + B 2 2 − 2 B − 2 + 4
= 4 + 1 2 A 2 + B 2 − 2 A + B = 4 + 1 2 t 1 2 + t 2 2 − 2 t 1 + t 2



