
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

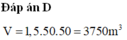

a) Khối lượng muối có trong hồ là: \(200.10 = 2000\left( {kg} \right)\).
Sau \(t\) phút kể từ khi bắt đầu bơm, lượng nước trong hồ là: \(200 + 2t\left( {{m^3}} \right)\).
Nồng độ muối tại thời điểm \(t\) phút kể từ khi bắt đầu bơm là: \(C\left( t \right) = \frac{{2000}}{{200 + 2t}}\left( {kg/{m^3}} \right)\)
b) \(\mathop {\lim }\limits_{t \to + \infty } C\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{200 + 2t}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{t\left( {\frac{{200}}{t} + 2} \right)}} = \mathop {\lim }\limits_{t \to + \infty } \frac{1}{t}.\mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{\frac{{200}}{t} + 2}}\)
\( = \mathop {\lim }\limits_{t \to + \infty } \frac{1}{t}.\frac{{\mathop {\lim }\limits_{t \to + \infty } 2000}}{{\mathop {\lim }\limits_{t \to + \infty } \frac{{200}}{t} + \mathop {\lim }\limits_{t \to + \infty } 2}} = 0.\frac{{2000}}{{0 + 2}} = 0\)
Ý nghĩa: Khi \(t\) càng lớn thì nồng độ muối càng dần về 0, tức là đến một lúc nào đó nồng độ muối trong hồ không đáng kể, nước trong hồ gần như là nước ngọt.

b: SA vuông góc (ABCD)
=>SA vuông góc AC
=>ΔSAC vuông tại A
c: AC=căn a^2+a^2=a*căn 2
=>SC=căn SA^2+AC^2=a*căn 5
SD=căn SA^2+AD^2=2a
Vì DS^2+DC^2=SC^2
nên ΔSDC vuông tại D

Chọn D
Khối đa diện ABCDSH được chia thành hai khối chóp S.ABCD và H.SCD

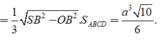
Vì H là điểm đối xứng của O qua SM nên
![]()

Vậy thể tích khối đa diện cần tính bằng
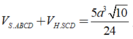

Đáp án B
Ta có
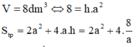
Ta tìm điều kiện của a đê diện tích toàn phần nhỏ nhất. xét hàm số ta được a=2