Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(S=\left(30-x\right)\left(40-x\right)\)
\(=\left(x-30\right)\left(x-40\right)=x^2-70x+1200\)
=>S không là hàm số bậc nhất đối với x
\(P=2\left[30-x+40-x\right]=2\left(70-2x\right)=-4x+140\)
=>P là hàm số bậc nhất đối với x
b: Khi x=0 thì \(P=-4\cdot0+140=140\)
Khi x=1 thì \(P=140-4=136\)
Khi x=2 thì \(P=140-8=132\)
Khi x=3 thì \(P=140-12=128\)
Khi x=4 thì P=140-4*4=124

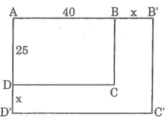
Sau khi tăng kích thước của mỗi chiều, ta được hình chữ nhật A’B’C’D’ có chiều dài A’B’ = (40 + x) cm, chiều rộng B’C’ = (25 + x) cm.
Các giá trị tương ứng của P:
| x | 0 | 1 | 1,5 | 2,5 | 3,5 |
| P = 4x + 130 | 130 | 134 | 136 | 140 | 144 |

- Gọi hình chữ nhật ban đầu ABCD có kích thước AB = 30cm; BC = 20cm.
- Sau khi bớt các kích thước của hình chữ nhật đi x (cm), ta có hình chữ nhật mới là A'B'C'D' có:
A'B' = 30 – x
B'C' = 20 – x
Gọi y là chu vi của hình chữ nhật A'B'C'D', ta có:
y = 2[(30 - x) + (20 - x)]
=> y = 2(50 - 2x)
=> y = -4x + 100 (cm)
Khi bớt mỗi kích thước x (cm) thì được một hình chữ nhật có các kích thước
là 20 – x (cm) và 30 – x (cm).
Khi đó chu vi của hình chữ nhật là y=2(20–x+30–x)y=2(20–x+30–x)
hay y=100–4x

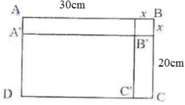
- Gọi hình chữ nhật ban đầu ABCD có kích thước AB = 30cm; BC = 20cm.
- Sau khi bớt các kích thước của hình chữ nhật đi x (cm), ta có hình chữ nhật mới là A'B'C'D' có:
A'B' = 30 – x
B'C' = 20 – x
Gọi y là chu vi của hình chữ nhật A'B'C'D', ta có:
y = 2[(30 - x) + (20 - x)]
=> y = 2(50 - 2x)
=> y = -4x + 100 (cm)

Sau khi tăng kích thước của mỗi chiều, ta được hình chữ nhật A’B’C’D’ có chiều dài A’B’ = (40 + x) cm, chiều rộng B’C’ = (25 + x) cm.
Diện tích hình chữ nhật mới:
S = (40 + x)(25 + x) = 1000 + 65x + x 2
S không phải là hàm số bậc nhất đối với x vì có bậc của biến số x là bậc hai.
Chu vi hình chữ nhật mới:
P = 2.[(40 + x) + (25 + x)] = 4x + 130
P là hàm số bậc nhất đối với x có hệ số a = 4, hệ số b = 130.