Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích bề mặt là `100π => 4π r^2 = 100π => r = 5 (m)`
Thể tích của hình cầu là:
`V=4/3 . π . r^3 = 4/3 . π . 5^3 =500/3 π (m^3)`

a, Tính được S = 64π c m 2 và V = 256 π 3 c m 3
b, Tính được S = 211,32π c m 2

Bán kính hình cầu :
\(4\pi r^2=100\pi\Rightarrow r=5cm\)
Thể tích hình cầu
\(S=\dfrac{4}{3}\pi r^3=\dfrac{4}{3}.\pi.5^3=\dfrac{500}{3}\pi\)
có \(S\)(bề mặt)\(=4\pi R^2=100\pi=>R=\sqrt{\dfrac{100\pi}{4\pi}}=5cm\)
\(=>V\)(cầu)\(=\dfrac{4}{3}\pi R^3=\dfrac{4}{3}.5^3.\pi=\dfrac{500}{3}\pi\left(cm^3\right)\)

Một hình cầu có số đo diện tích (đơn vị: m2) bằng số đo thể tích (đơn vị: m3). Tính bán kính hình cầu, diện tích mặt cầu và thể tích hình cầu.
Hướng dẫn làm bài:
Gọi R là bán kính hình cầu (đơn vị : mét)
Khi đó ta có: S = 4πR2 và V=4/3 πR3
Theo đề bài ta có: 4πR2=4/3πR3⇒R/3=1⇒R=3(m)
Ta có: S = 4πR2 = 4π . 32 = 36π (m2)
V=4/3 π R3=4/3 π.33=36π(m3)


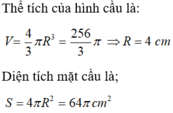
Tính được V = 500 3 πm 3