Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

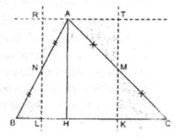
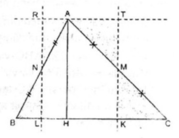
MB < MC => SABM < SACM => Điểm N là giao của đường thẳng d thỏa mãn đề bài với cạnh AC, nằm trong AC. Gọi I là trung điểm AC. Lúc đó SMNC = SBCI . Gọi P, Q tương ứng là hình chiều của I, N trên BC. => IP/NQ = BC/CM = CP/CQ . B, C, I, P cố định => xác định được Q từ đó tìm ra N.
????
Mình không hiểu câu trả lời của bạn Hà Chí Trung cho lắm

a,Chứng minh tam giác MPE đồng dạng với tam giác KPQ.
+PK là phân giác góc QPO.
=>^MPE = ^KPQ.(α) .
+ Tam giác OMN đều .=>^EMP=120 độ.
+ QK cũng là phân giác ^OQP.
=>^QKP = 180 - (^KQP+^KPQ).
Mà 2^KQP + 2^KPQ =180- 60 =120 độ.
=>^QKP=120 độ. Do đó:^EMP = ^QKP. (ß) .
Từ (α) và (ß), ta có tam giác MPE đồng dạng với tam giác KPQ.
b, Chứng minh tứ giác PQEF nội tiếp được trong đường tròn.
Do hai tam giác MPE và KPQ đồng dạng nên:^MEP=^KQP , hay: ^FEP=^FQP.
Suy ra, tứ giác PQEF nội tiếp được trong đường tròn.
c, Gọi D là trung điểm của đoạn PQ. Chứng minh tam giác DEF là một tam giác đều.
Do hai tam giác MPE và KPQ đồng dạng nên: PM/PK =PE/PQ . Suy ra: PM/PE =PK/PQ .
Ngoài ra: ^MPK=^EPQ . Do đó, hai tam giác MPK và EPQ đồng dạng.
Từ đó:^PEQ=^PMK=90độ .
Suy ra, D là tâm của đường tròn ngoại tiếp tứ giác PQEF.
Vì vậy, tam giác DEF cân tại D.
Ta có: ^FDP=2^FQD=^OQP ; ^EDQ=2^EPD=^OPQ .
^FDE=180 - (^FDP+^EDQ) =^POQ =60độ.
Từ đó, tam giác DEF là tam giác đều.

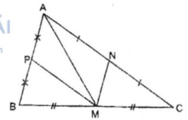
Tương tự như trên câu b.
Xét Δ ABC. Gọi M là trung điểm của BC
N là trung điểm của AC, P là trung điểm của AB
Cắt tam giác ABC theo đường AM ta có hai phần có diện tích bằng nhau
Cắt tam giác AMC theo đường AN ta có hai phần có diện tích bằng nhau
Cắt tam giác AMB theo đường MP ta có hai phần diện tích bằng nhau, ta có diện tích bốn phần chia bằng nhau.

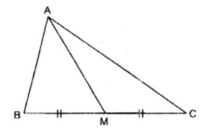
Ta đã biết hai tam giác có cạnh đáy bằng nhau và chung chiều cao thì có diện tích bằng nhau. Giả sử △ ABC. Gọi M là trung điểm của BC
Cắt tam giác ABC theo đường AM chia tam giác ABC ra hai phần có diện tích bằng nhau.