Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi x là số sản phẩm làm được trong 1 ngày thì thời gian quy định là \(\frac{600}{x}\)với x>0
thời gian làm được 400 sản phẩm là \(\frac{400}{x}\)ngày
thời gian quy định còn lại là \(\frac{600}{x}\)-\(\frac{400}{x}\)=\(\frac{200}{x}\)
sản phẩm làm được trong 1 ngày với năng suất mới là x+10
=>thời gian làm với năng suất mới là\(\frac{200}{x+10}\)
vì sớm hơn quy định 1 ngày nên ta có pt
\(\frac{200}{x}\)-1=\(\frac{200}{x+10}\)
<=>\(\frac{200-x}{x}=\)\(\frac{200}{x+10}\)
<=>\(\left(200-x\right)\left(x+10\right)=200x\)
<=>\(200x-10x-x^2+2000-200x=0\)
<=>-x2-10x+2000=0
<=>-\(\left(x^2+10x+25\right)+25+2000=0\)
<=>-\(-\left(x+5\right)^2=-2025\)
<=>\(\left(x+5\right)^2=2025\)
<=>x+5=45 vì x>0
<=>x=40
số sản phẩm làm được trong 1 ngày là 40 sản phẩm
tick nha

Gọi số sản phẩm đội dự định làm mỗi ngày là x (x ∈ ℕ * , x < 84) (sản phẩm)
*) Theo kế hoạch, thời gian hoàn thành là 1000/x (ngày)
*) Thực tế, mỗi ngày làm được x + 10 (sản phẩm)
Thời gian hoàn thành 1000/(x+10) (ngày)
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
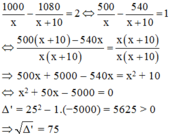
Phương trình có hai nghiệm phân biệt: x 1 = − 25 – 75 = −100 (loại)
và x 2 = −25 + 75 = 50 (tmđk)
Vậy theo kế hoạch, mỗi ngày tổ dự định làm 50 sản phẩm
Đáp án: C

Gọi số sản phẩm làm theo kế hoạch mỗi ngày là x>0 và số ngày dự định là y>0
Ta có: \(xy=200\)
4 ngày đầu làm được: \(4x\) sản phẩm
Những ngày còn lại: \(\left(y-6\right)\left(x+10\right)\)
Theo bài ra ta có hệ:
\(\left\{{}\begin{matrix}xy=200\\4x+\left(y-6\right)\left(x+10\right)=200\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=200\\5y-x=30\end{matrix}\right.\)
\(\Rightarrow y\left(5y-30\right)=200\)
\(\Leftrightarrow y^2-6y-40=0\Rightarrow\left[{}\begin{matrix}y=10\\y=-4\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x=\dfrac{200}{10}=20\)

Lời giải:
Gọi thời gian dự kiến là $a$ ngày thì năng suất dự kiến là $\frac{130}{a}$ sản phẩm / ngày.
Theo bài ra ta có:
Năng suất thực tế: $\frac{130}{a}+2$
Thời gian thực tế: $a-2$
Sản lượng thực tế: $(\frac{130}{a}+2)(a-2)=130+2$
$\Leftrightarrow a-\frac{130}{a}=3$
$\Leftrightarrow a^2-3a-130=0$
$\Rightarrow a=13$ (chọn) hoặc $a=-10$ (loại)
Vậy thời gian dự kiến là $13$ ngày.

a) Ta có AH là đường cao của tam giác ABC, do đó AB là đường trung trực của đoạn thẳng LH (vì H là trung điểm của BC).
b) Ta có $\angle AED = \angle ACD$ do cùng chắn cung AD trên đường tròn (T). Mà $\angle A = \angle APQ$ vì DE // PQ, nên $\angle AED = \angle APQ$. Tương tự, ta cũng có $\angle ADE = \angle AQP$. Do đó tam giác ADE và APQ đều có hai góc bằng nhau, tức là cân.
c) Ta có $\angle LBD = \angle LCB$ do cùng chắn cung LB trên đường tròn (T). Mà $\angle LCB = \angle LPB$ vì DE // PQ, nên $\angle LBD = \angle LPB$. Tương tự, ta cũng có $\angle LDC = \angle LQC$. Do đó tam giác LBD và LPQ đều có hai góc bằng nhau, tức là đồng dạng. Vậy ta có $\frac{LD}{LP} = \frac{LB}{LQ}$.
Từ đó, có $\frac{LP}{LQ} = \frac{LB}{LD}$. Áp dụng định lý cosin trong tam giác BPQ, ta có:
$PQ^2 = BP^2 + BQ^2 - 2BP \cdot BQ \cdot \cos{\angle PBQ}$
Nhưng ta cũng có:
$BP = LB \cdot \frac{LD}{LP}$
$BQ = L \cdot \frac{LP}{LD}$
Thay vào định lý cosin, ta được:
$PQ^2 = LB^2 + LQ^2 - 2LB \cdot LQ \cdot \frac{LD}{LP} \cdot \frac{LP}{LD} \cdot \cos{\angle PBQ}$
$PQ^2 = LB^2 + LQ^2 - 2LB \cdot LQ \cdot \cos{\angle PBQ}$
Tương tự, áp dụng định lý cosin trong tam giác ADE, ta có:
$DE^2 = AD^2 + AE^2 - 2AD \cdot AE \cdot \cos{\angle AED}$
Nhưng ta cũng có:
$AD = LD \cdot \frac{LB}{LP}$
$AE = LQ \cdot \frac{LD}{LP}$
Thay vào định lý cosin, ta được:
$DE^2 = LD^2 + LQ^2 - 2LD \cdot LQ \cdot \frac{LB}{LP} \cdot \frac{LD}{LP} \cdot \cos{\angle AED}$
$DE^2 = LD^2 + LQ^2 - 2LD \cdot LQ \cdot \cos{\angle AED}$
Nhưng ta cũng có $\angle AED = \angle PBQ$ do tam giác cân ADE và APQ, nên $\cos{\angle AED} = \cos{\angle PBQ}$. Do đó,
$DE^2 + PQ^2 = 2(LB^2 + LQ^2) - 4LB \cdot LQ \cdot \cos{\angle PBQ}$
Nhưng ta cũng có $LB \cdot LQ = LH \cdot LL'$ (với L' là điểm đối xứng của L qua AB), do tam giác HL'B cân tại L'. Thay vào phương trình trên, ta được:
$DE^2 + PQ^2 = 2(LB^2 + LQ^2) - 4LH \cdot LL' \cdot \cos{\angle PBQ}$

gọi x là số sản phẩm làm 1 ngày theo dự định
3200/x là số ngày làm 3200 sp theo dự định
5+(3200-5x)/(x+40) là số ngày làm xong sản phẩm thực tê
ta có pt
3200/x-3=(5+(3200-5x)/(x+40))