Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình:
Giải:
Có điểm I là trung điểm của AC
\(\Leftrightarrow IC=\dfrac{1}{2}AC\)
Lại có điểm K là trung điểm của ABC
\(\Leftrightarrow KC=\dfrac{1}{2}CB\)
Vì điểm C nằm giữa hai điểm A và B Mà I và K lần lượt là trung điểm của AC và CB Nên điểm C đồng thời nằm giữa điểm I và điểm K Ta có đẳng thức: \(IC+CK=IK\) \(\Leftrightarrow\dfrac{1}{2}AC+\dfrac{1}{2}CB=IK\) \(\Leftrightarrow\dfrac{1}{2}\left(AC+CB\right)=IK\) \(\Leftrightarrow\dfrac{1}{2}.18=IK\) \(\Leftrightarrow IK=9\left(cm\right)\) Vậy ...
từ điểm giữa I của AC đến điểm giữa K của CB là như thế nào???

a) xét tam giác AIB và tam giác CID có:
AI=IC (GT)
góc AIB= góc CID (2 góc đối đỉnh)
BI=ID (GT)
suy ra tam giác AIB và tam giác CID (CGC)
suy ra góc BAC = góc ACD (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong
suy ra AB//CD
b) xét tam giác AID và tam giác CIB có:
IA=IC (GT)
góc AID = góc BIC (2 góc so le trong)
IB=ID (GT)
suy ra tam giác AID= tam giác CIB (CGC)
suy ra góc ADB= góc DBC (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong
suy ra AD//CD
c) vì tam giác AID = tam giác CIB (CMT)
suy ra AD=BC (2 góc tương ứng)

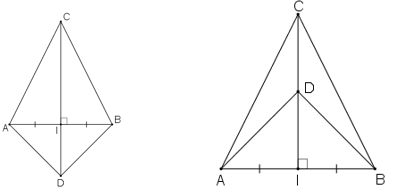
Xét tam giác ACI và tam giác BCI , có
CI là cạnh chung
AC = BC
AI= BI
=> tam giác ACI = tam giác BCI
Xét tam giác ACD và tam giác BCD , có
CD là cạnh chung
AD = BD
AC =BC
=> tam giác ACD = tam giác BCD
Xét tam giác ADI và tam giác BDI , có
DI là cạnh chung
AD = BD
AI = BI
=> tam giác ADI = tam giác BDI
ok 3 cặp nha thư
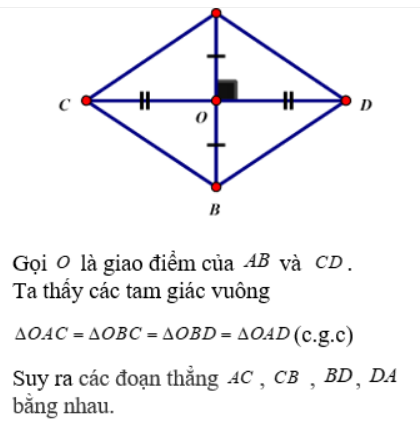
Có hai trường hợp:
+ ΔAIC = ΔBIC (c.g.c) vì:
AI = IB (gt)
∠AIC = ∠BIC = 90o
CI chung.
+ ΔAID = ΔBID(c.g.c) vì:
AI = ID (gt)
∠AID = ∠BID = 90o
DI chung.
+ ΔACD = ΔBCD(c.c.c) vì:
AC = BC (Lấy từ ΔAIC = ΔBIC)
AD = BD (Lấy từ ΔAID = ΔBID)
CD chung

a Đặt tên điểm nằm giữa là I nhé. Vì 2 đoạn thẳng AB và CD cắt nhau tại trung điểm nên suy ra 2 cạnh IC=ID Sau đó xét tam giác bằng nhau trường hợp cạnh-góc-cạnh và suy ra các đoạn thảng bằng nhau b Vì AB và CD vuông góc suy ra góc AID = 90 độ, xong tính các góc kia cũng ra 90 độ bằng cách 2 góc kề bù rồi chia 2 là ra tia p/g

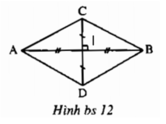
+ Gọi giao điểm của AB và CD là I. Theo giả thiết I là trung điểm của CD và AB.
+) Xét tam giác ACI và tam giác ADI có:
AI chung
CI = DI (vì I là trung điểm của CD).
∠AIC = ∠ DIA = 90º ( vì AB vuông góc với CD tại I).
Suy ra: ∆ ACI = ∆ ADI (c.g.c)
Suy ra: ∠CAI = ∠ ADI ( hai góc tương ứng).
Do đó, AB là tia phân giác của góc ∠CAD .
+) Chứng minh tương tự ta có: CD là tia phân giác của góc C, BA là tia phân giác của góc B, DC là tia phân giác của góc D.

Coi giá bán ngày thường là 100% thì giá bán ngày 1 - 6 là:
100% - 10% = 90%
Cửa hàng vẫn còn lãi 8% tức là cửa hàng bán được: 100% + 8% = 108% (giá mua)
Số tiền lãi tính theo giá mua là:
100 : 90 x 108 = 120% (giá mua)
Vậy ngày thường thì cửa hàng lãi được:
120% - 100% = 20%
Ta có:
AC + CB = AB = 18cm
mà AC = AM + MC = 2MC (vì M là trung điểm AC nên AM = MC)
CB = CQ + QB = 2CQ (vì Q là trung điểm CB nên CQ = QB)
=> 2MC + 2CQ = AB = 18cm
<=> 2 (MC + CQ) = 18cm
<=> MC + CQ = 9cm