Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giá trị của biến trở để công suất tỏa nhiệt trên biến trở là cực đại R 0 = r 2 + Z L 2 = 25 Ω.
→ Khi thay đổi biến trở từ 10 Ω đến 20 Ω thì công suất tỏa nhiệt luôn tăng.
Đáp án C

Hai giá trị của R cho cùng công suất tiêu thụ trên mạch thõa mãn R 1 R 2 = R 0 2 = Z L − Z C 2
→ Hệ số công suất
cos φ = R R 2 + Z L − Z C 2 ⇒ cos φ 1 = R 1 R 1 2 + R 1 R 2 = 0 , 6 cos φ 1 = R 2 R 2 2 + R 1 R 2 = 0 , 8 .
Đáp án B

Đáp án D
R thay đổi, công suất bằng nhau nên có công thức R 1 R 2 = ( Z L − Z C ) 2
Khi R = R1 = 15Ω : P = U 2 R 1 Z 1 2 = U 2 R 1 R 1 2 + R 1 R 2 = U 2 R 1 + R 2 (1)
Khi R = R0 : P m ax = U 2 2 R 0 R 0 = Z L − Z C ⇒ R 0 = 30 ( Ω ) (2)
Từ (1) và (2) suy ra P m ax P = R 1 + R 2 2 R 0 ⇒ P m ax = 375 ( W )

Đáp án D
R thay đổi, công suất bằng nhau nên có công thức ![]()
Khi R = R1 = 15Ω 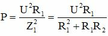 (1)
(1)
Khi R = R0 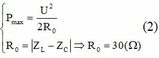
Từ (1) và (2) suy ra 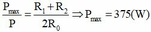

+ Với f = 50 Hz ® ZL = 70 W, ZC = 100 W.
+ Công suất tỏa nhiệt trên biến trở là:
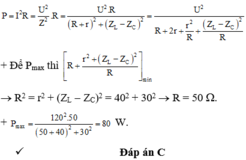

Đáp án C
+ Hai giá trị của R cho cùng công suất tiêu thụ trên mạch R 1 R 2 = ( Z L - Z C ) 2 = R 0 2 , với R 0 là giá trị của biến trở để công suất tiêu thụ trên mạch là cực đại
![]()
+ Ta có:
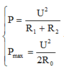
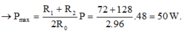

Đáp án B
+ Điều chỉnh R để công suất trên biến trở đạt cực đại ![]()
+ Tổng trở của đoạn mạch AB là ![]()
![]()
Để Z chia hết cho 40 thì: ![]() = số nguyên → r phải là bội số của 10 : r=10k
= số nguyên → r phải là bội số của 10 : r=10k
+ Hệ số công suất của đoạn mạch AB là: 

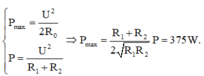

Công suất tỏa nhiệt trên biến trở cực đại khi R = r 2 + Z L 2 = 40 Ω.
Đáp án D