Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tham khảo:
a) Ta có: \(M = {a^{{{\log }_a}M}},N = {a^{{{\log }_a}N}} \Rightarrow MN = {a^{{{\log }_a}M}}.{a^{{{\log }_a}N}} = {a^{{{\log }_a}M + {{\log }_a}N}}\)
Mặt khác: \(MN = {a^{{{\log }_a}\left( {MN} \right)}}\)
Vậy \({a^{{{\log }_a}M + {{\log }_a}N}} = {a^{{{\log }_a}\left( {MN} \right)}} \Leftrightarrow {\log _a}M + {\log _a}N = {\log _a}\left( {MN} \right)\)
b)
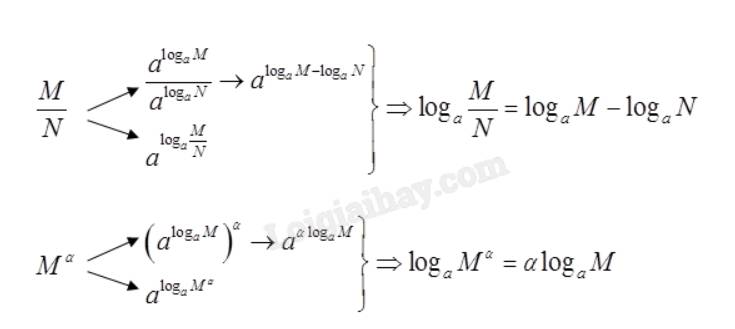
Gọi \(B_1\) là biến cố "sinh viên A đạt môn thứ nhất"
\(B_2\) là biến cố "sinh viên A đạt môn thứ hai"
\(\Rightarrow P\left(B_1\right)=0,8\) ; \(P\left(B_2|B_1\right)=0,6\) ; \(P\left(B_2|\overline{B_1}\right)=0,3\)
a/ Xác suất đạt môn thứ hai:
\(P\left(B_2\right)=P\left(B_1\right).P\left(B_2|B_1\right)+P\left(\overline{B_1}\right)P\left(B_2|\overline{B_1}\right)\)
\(=0,8.0,6+0,2.0,3=0,54\)
b/ Xác suất để đạt ít nhất 1 môn:
\(P\left(B_1\cup B_2\right)=P\left(B_1\right)+P\left(B_2\right)-P\left(B_1B_2\right)\)
\(=P\left(B_1\right)+P\left(B_2\right)-P\left(B_1\right)P\left(B_2|B_1\right)=0,86\)
Chọn A
Có 
cách chia 20 bạn vào 4 nhóm, mỗi nhóm 5 bạn.
- Gọi A là biến cố “ 5 bạn nữ vào cùng một nhóm”
- Xét 5 bạn nữ thuộc nhóm A có 
cách chia các bạn nam vào các nhóm còn lại.
- Do vai trò các nhóm như nhau nên có 
Khi đó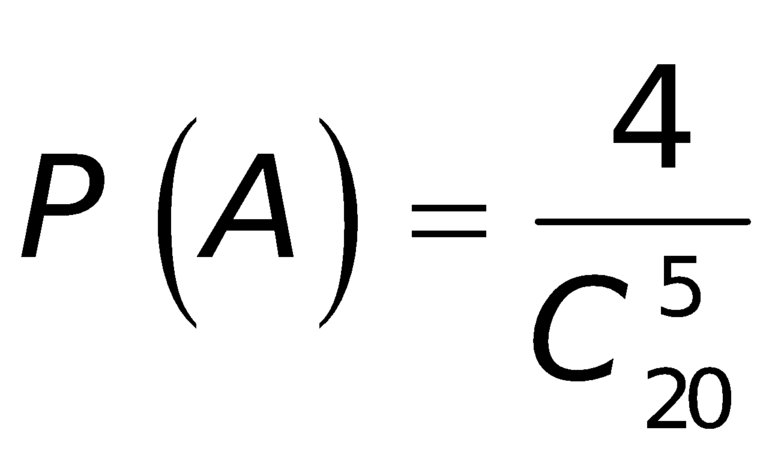 
.
a) M(-1;1) đối xứng qua trục Oy ta được N(-1;1).
Gọi M'(x;y) là ảnh của N(-1;1) qua phép tịnh tiến theo vectơ v → = ( 2 ; 0 )
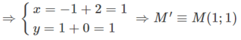
b) Gọi P(x;y) là ảnh của M(1;1) qua phép tịnh tiến theo v → = ( 2 ; 0 )
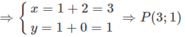
P(3;1) đối xứng qua trục Oy ta được M"(-3;1)
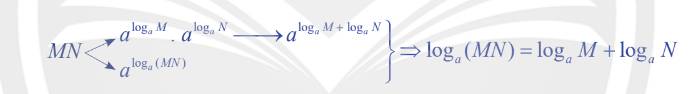
Chọn C
Theo quy tắc nhân ta có số cách là mn