Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
n(omega)=12!
A: "Xếp các học sinh thành 1 hàng ngang sao cho ko có 2 học sinh nữ nào đứng cạnh nhau"
=>\(n\left(A\right)=8!\cdot A^4_9\)
=>P=14/55
Đáp án A
Số cách lấy ra 4 ứng viên bất kỳ từ 16 ứng viên là 
cách.
- Gọi A là biến cố “4 ứng viên lấy được có đúng một ứng viên 10 tuổi và không quá hai ứng viên 12 tuổi”. Ta xét ba khả năng sau:
- Số cách lấy 1 10 tuổi, 3 11 tuổi là: 
- Số cách lấy 1 10 tuổi, 2 11 tuổi, 1 12 tuổi là: 
- Số cách lấy 1 10 tuổi, 1 11 tuổi, 2 12 tuổi là: 
Xác suất của biến cố A là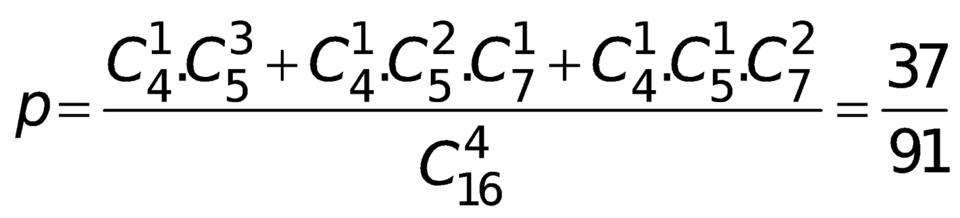 
.
Đáp án B.
Số cách chọn 5 em học sinh từ 8 học sinh trên là 
cách
- Để chọn 5 em thỏa mãn bài ra, ta xét các trường hợp sau
+) 1 nam khối 11, 1 nữ khối 12 và 3 nam khối 12 có 
cách
+) 1 nam khối 11, 2 nữ khối 12 và 2 nam khối 12 có 
cách
+) 2 nam khối 11, 1 nữ khối 12 và 2 nam khối 12 có 
cách
+) 2 nam khối 11, 2 nữ khối 12 và 1 nam khối 12 có 
cách
- Số cách chọn 5 em thỏa mãn bài ra là:
cách
Vậy xác suất cần tính là: 
TH1: Chọn 3 nam,1 nữ có: \(C^3_5.C^1_4=40\) cách
TH2: Chọn 2 nam, 2 nữ có: \(C^2_5.C^2_4=60\) cách
TH3: Chọn 1 nam, 3 nữ có: \(C^1_5.C^3_4\)=20 cách
Vậy có 40+60+20=120 cách để chọn
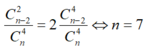
Đã có 1 nữ được tuyển nên số nữ còn lại là 4-1=3 và số người còn lại là 6-1=5(người)
Số cách chọn 1 người trong 5 người còn lại là: 5(cách)
=>Xác suất để Hoa trúng tuyển là \(P=\dfrac{1}{5}\)=20%