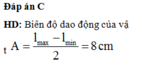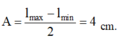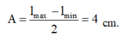Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
+ Biên độ dao động của vật A = l max − l min 2 = 4 cm

Bạn xem thêm phần lí thuyết ở đây nhé: Con lắc lò xo treo thẳng đứng | Học trực tuyến
\(\omega=2\pi f = 9\pi (rad/s)\)
Có \(\omega=\sqrt{\dfrac{g}{\Delta \ell_0}}\) với \(\Delta \ell_0\) là độ biến dạng của lò xo khi vật ở vị trí cân bằng.
\(\Rightarrow \Delta \ell_0=\dfrac{g}{\omega^2}=\dfrac{10}{(9\pi)^2}=0,012(m)=1,2(cm)\)
Chiều dài lò xo khi vật ở VTCB là: \(\ell_{CB}=\dfrac{40+56}{2}=48(cm)\)
Có: \(\ell_{CB}=\ell_0+\Delta\ell_0\Rightarrow \ell_0=48-1,2=46,8(cm)\)
Vậy chiều dài tự nhiên của lò xo là 46,8 cm.

Đáp án A
Phương pháp: Áp dụng công thức chiều dài nhỏ nhất và lớn nhất của con lắc lò xo treo thẳng đứng
Cách giải :
Ở VTCB lò xo dãn một đoạn:
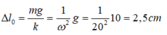
Khi ở VTCB lò xo có chiều dài: l c b = 30 + 2,5 = 32,5 cm
Biên độ dao động A = 2 cm nên chiều dài nhỏ nhất và lớn nhất lần lượt là
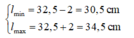

Biên độ dao động của con lắc là
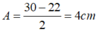
Áp dụng định luật bảo toàn năng lượng ta có
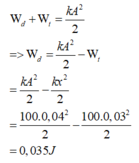
Đáp án D

Đáp án A
Biên độ dao động của con lắc A = l m a x − l min 2 = 30 − 22 2 = 4 cm
→ Động năng của con lắc tại vị trí có li độ x
E d = E − E t = 1 2 k A 2 − x 2 = 1 2 .100. 0 , 04 2 − 0 , 03 2 = 0 , 035 J