Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
W t = 1 2 k x 2 = 1 2 m . w 2 x 2 = 1 2 m . w 2 . ( A 2 ) 2 = W 4 → W đ = 3 W 4
=> Tỉ số giữa động năng và thế năng của con lắc là 3.

Ta có :
\(\dfrac{W_t}{W}=\dfrac{\dfrac{1}{2}kx^2}{\dfrac{1}{2}kA^2}=\dfrac{x^2}{A^2}=\dfrac{5^2}{10^2}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{W_t}{W_t+W_đ}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{W_đ}{W_t}=3\)
Vậy...

Đáp án C
Phương pháp: Sử dụng đường tròn lượng giác
Cách giải:
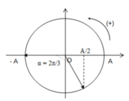
Biểu diễn bằng hình vẽ ta được thời gian ngắn nhất vật đi từ vị trí x1 = - A đến x2 = A/2 tương ứng với góc quét α = 2π/3 => Thời gian t = α/ω = T/3 = 1s => T = 3s.

Chọn A
Tại thời điểm cố định lò xo ta có E d = n E t E d + E t = E → E t = E n + 1 E d = n E n + 1
+ Vì thế năng đàn hồi của lò xo phân bố đều trên mỗi đơn vị chiều dài, do vậy thế năng của hệ dao động mới là E ' t = E t m = E m n + 1
+ Cơ năng của hệ dao động mới: E ' = E ' t + E ' d = E m n + 1 + n E n + 1 = 1 2 k ' A ' 2
Trong đó k′ = mk là độ cứng của phần lò xo tham gia vào dao động của vật lúc sau.
→ Biến đổi toán học ta thu được tỉ số A ' A = m n + 1 2 m n + 1

Đáp án B
Ta có E d = 1 3 E t → x = ± 3 2 A trong một chu kì khoảng thời gian E d ≥ E t 3 là Δ t = T 3 = 1 3 s → T = 1 s.
Kết hợp với: x A 2 + v ω A 2 = 1 v = ω x → x = 2 2 A
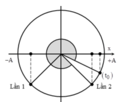
Tại t = 0, vật đi qua vị trí x = 3 2 A , theo chiều dương. Biểu diễn các vị trí tương ứng trên đường tròn
Trong một chu kì vật đi qua vị trí thoãn mãn yêu cầu bài toán 2 lần → tách 2016 = 2014 + 2
Vậy tổng thời gian là Δ t = t φ + 1007 T = 23 24 + 1007 = 1007 , 958 s
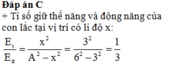


Theo đề bài: \(\dfrac{x}{A}=\dfrac{5}{10}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{W_t}{W}=\dfrac{\dfrac{1}{2}kx^2}{\dfrac{1}{2}kA^2}=\dfrac{1}{4}\)
\(\Rightarrow W=4W_t\)
Mà cơ năng của con lắc: \(W=W_t+W_đ\)
\(\Rightarrow4W_t=W_t+W_đ\)
\(\Rightarrow\dfrac{W_t}{W_đ}=\dfrac{1}{3}\)