Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giải thích: Đáp án B
Phương pháp:
+ Sử dụng công thức tính chu kì của con lắc đơn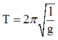 
+ Sử dụng líthuyết về con lắc chịu tác dụng của lực điện trường.
Cách giải:
+ Chiều dài của con lắc là l.
Khi chiều dài là l → chu kì dao động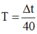 
Khi chiều dài là l + 7,9cm → chu kì dao động
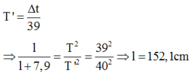
+ Con lắc có chiều dài tăng thêm là l’ = l + 7,9 cm = 160 cm, tích thêm điện tích q = -108 C
Theo đề bài: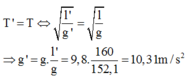 
NX: g’ > g mà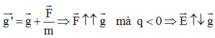 
hay
E
⇀
thẳng đứng hướng lên.
Và: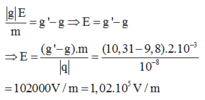 
\(T_1=\frac{\Delta t}{40}.\)
\(T_2=\frac{\Delta t}{39}.\)
=> \(\frac{T_1}{T_2}=\frac{40}{39}=\sqrt{\frac{l_1}{l_2}}\).
Khi cho quả cầu tích điện và đặt điện trường vào thì gia tốc biểu kiến của con lắc lúc này là \(\overrightarrow{g_{bk}}=\overrightarrow{g}+\frac{\overrightarrow{F_đ}}{m}=\overrightarrow{g}+\frac{\overrightarrow{E}q}{m}\)
Do để chu kì không đổi khi tăng chiều dài thì g cũng phải tăng như vậy \(g_{bk}=g+\frac{E}{m}=g+\frac{Eq}{m}\)
Để \(T_1=T_2\)
=>\(2\pi\sqrt{\frac{l_2}{g_{bk}}}=2\pi\sqrt{\frac{l_1}{g}}\)
=> \(\frac{l_2}{l_1}=\frac{g+\frac{Eq}{m}}{g}=\frac{40^2}{39^2}.\)
=> \(E=2,08.10^4V.\)
- Góc lệch của dây treo VTCB:
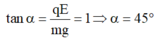
Gia tốc trong trường biểu kiến:
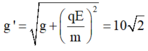
- Khi kéo lệch khỏi VTCB một góc 54° so với phương thẳng đứng thì α = 9° (góc lệch dây treo tại VTCB mới)
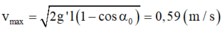
Đáp án A
Góc lệch của dây treo VTCB :
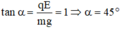
Gia tốc trong trường biểu kiến
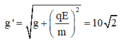
Khi kéo lệch khỏi VTCB một góc 54 ° so với phương thẳng đứng thì
(góc lệch dây treo tại VTCB mới)
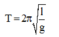
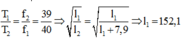
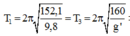
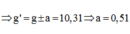
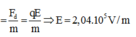
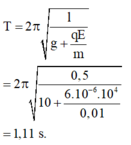
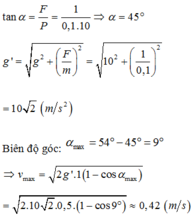
Giải thích: Đáp án D
Phương pháp: Sử dụng công thức tính chu kì của con lắc đơn dao động điều hoà và sử dụng lí thuyết về bài toán con lắc đơn chịu tác dụng của lực điện trường.
Cách giải:
Để a ⇀ ; g ⇀ cùng hướng, q > 0 thì E ⇀ hướng xuống