Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có:
nm//ac
bm=cm
=>bn=na
=>nm là đtb của tam giác bac
=>nm = ca/2=0,4
vậy khoảng cánh chân của người đứng trên bật than đối với bức tường là 0,4 m

P/s:mình vẽ hình rồi đặt tên luôn cho tam giác.
Xét ΔABC và ΔMNP ta có
\(\widehat{ABC}=\widehat{MNP}=90^0\)
Vì toà nhà được chiếu ánh sáng cùng thời điểm \(\rightarrow\widehat{ACB}=\widehat{MPN}\)
⇒ ΔABC ∼ ΔMNP(gg )
⇒\(\dfrac{AB}{MN}=\dfrac{BC}{NP}hay\dfrac{AB}{3}=\dfrac{23}{65}\)
\(\Rightarrow AB=\dfrac{3.23}{6,5}=10,6\)(m)
Vậy toà nhà cao 10,6m
:v đề sai hay cậu sai đây nhỉ mà là 65 mà ta
với lại mình chưa hiểu lắm chỗ này á...
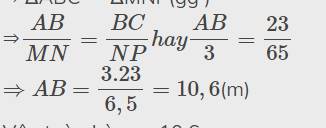
tỉ lệ thì đúng rồi mà lúc thay số vào lại là lạ à nhen:))
nếu cậu làm: \(\dfrac{AB}{MN}=\dfrac{BC}{NP}\)
ý cậu là AB là độ cao của toàn nhà, BC là bóng của toàn nhà;
MN là chiều cao cột sắt, NP là bóng của cột sắt (à mấy bài này cậu phải nêu cái này ra á không là trừ 0.25 điểm;))
như vậy thì AB=?, BC= 23 m, MN= 65m, NP= 3m nè thay vào thì được kết quả rất là lớn
Nên mình nghĩ là đề sai đó, mà làm sao mà 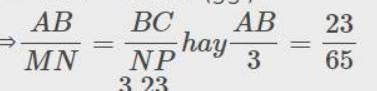
hai cái này nó tương đương được ha cậu, hay là mình chưa xem kĩ nhỉ?
MN đang là 65 thì thành 3, NP đang là 3 thì thành 65 cái này là cách biến đổi mới hả cậu ơi:(
mà mình thấy cậu làm bài nó hơi kì nhé:

Ủa vậy là 65 hay 6.5. Mình thấy số 6.5 cũng hợp lí mà dựa vào đâu cậu biết đó là số 6.5 mà tính đây? Hay thật đó!
Vậy là đề sai hay cậu sai nhỉ?

ΔABM đồng dạng với ΔCDM'
=>AB/CD=AM/CM'
=>AB=3*184,5/32=17,3(m)

Khoảng cách từ điểm gỗ chạm vào tường trên mặt đất là:
\(\sqrt{2,6^2-1^2}=2,4\left(m\right)\)

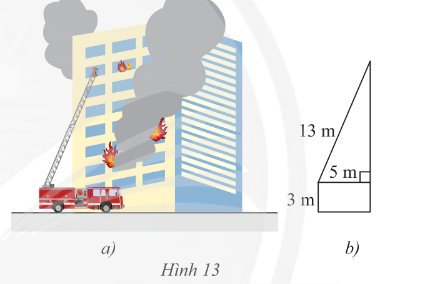
Gọi \(x\) là khoảng cách của xe đến đầu thang (m)
Áp dụng định lý Pythagore vào tam giác vuông trong hình ta có:
\({x^2} + {5^2} = {13^2}\)
\({x^2} = {13^2} - {5^2} = 144 = {12^2}\)
\(x = 12\) (m)
Chiều cao mà thang có thể vươn tới là:
\(12 + 3 = 15\) (m)

Cậu tham khảo đường link này là ra, dạng tương tự
https://h.vn/hoi-dap/tim-kiem?q=B%C3%A0i+53+(Sgk+t%E1%BA%ADp+2+-+trang+87)M%E1%BB%99t+ng%C6%B0%E1%BB%9Di+%C4%91o+chi%E1%BB%81u+cao+c%E1%BB%A7a+m%E1%BB%99t+c%C3%A2y+nh%E1%BB%9D+m%E1%BB%99t+c%E1%BB%8Dc+ch%C3%B4n+xu%E1%BB%91ng+%C4%91%E1%BA%A5t,+c%E1%BB%8Dc+cao+2m+v%C3%A0+%C4%91%E1%BA%B7t+xa+c%C3%A2y+15m.+Sau+khi+ng%C6%B0%E1%BB%9Di+%E1%BA%A5y+l%C3%B9i+ra+xa+c%C3%A1ch+c%E1%BB%8Dc+0,8m+th%C3%AC+nh%C3%ACn+th%E1%BA%A5y+%C4%91%E1%BA%A7u+c%E1%BB%8Dc+v%C3%A0+%C4%91%E1%BB%89nh+c%C3%A2y+c%C3%B9ng+n%E1%BA%B1m+tr%C3%AAn+m%E1%BB%99t+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng.+H%E1%BB%8Fi+c%C3%A2y+cao+bao+nhi%C3%AAu,+bi%E1%BA%BFt+r%E1%BA%B1ng+kho%E1%BA%A3ng+c%C3%A1ch+t%E1%BB%AB+ch%C3%A2n+ng%C6%B0%E1%BB%9Di+%E1%BA%A5y+%C4%91%E1%BA%BFn+m%E1%BA%AFt+ng%C6%B0%E1%BB%9Di+%E1%BA%A5y+l%C3%A0+1,6m+?&id=247547

Gọi tam giác tạo thành là tam giác ABC
Với chiếc thang là cạnh huyền AC, khoảng cách của chân thang và chân tường là BC và chiều cao của bức tường là AB:
Áp dụng định lý Py-ta-go ta có:
\(AC=\sqrt{BC^2+AB^2}=\sqrt{1,5^2+6^2}\approx6,2\left(m\right)\)
Độ dài của chiếc thang nhỏ:
\(A'C'=\dfrac{2}{3}\cdot AC=\dfrac{2}{3}\cdot6,2\approx4,13\left(m\right)\)
Áp dụng định lý Py-ta-go ta tìm được độ cao mà thang đặt đến:
\(A'B'=\sqrt{A'C'^2-B'C'^2}=\sqrt{4,13^2-1^2}\approx4\left(m\right)\)
Điểm cao nhất của thang cách mặt bước tường là:
\(AB-A'B'=6-4=2\left(m\right)\)
Vậy....