Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi \(200km/h = \frac{{500}}{9}m/s\)
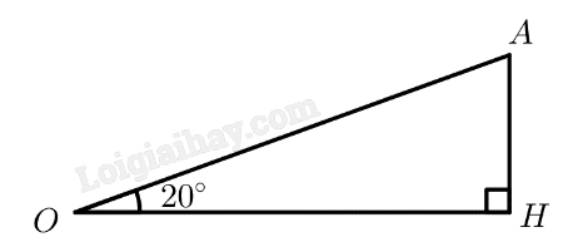
Mô hình hoá như hình vẽ, với \(OA\) là quãng đường máy bay bay được sau 2 giây, \(OH\) là độ cao của máy bay so với mặt đấy khi máy bay bay được sau 2 giây, độ lớn của góc \(\widehat {AOH}\) chỉ số đo góc giữa máy bay với mặt đất.
Sau 2 giây máy bay bay được quãng đường là: \(\frac{{500}}{9}.2 = \frac{{1000}}{9}\left( m \right)\)
Vì tam giác \(OAH\) vuông tại \(H\) nên ta có:
\(AH = OA.\sin \widehat {AOH} = \frac{{1000}}{9}.\sin {20^ \circ } \approx 38,0\left( m \right)\)
Vậy độ cao của máy bay so với mặt đất là 38 mét sau khi máy bay rời khỏi mặt đất 2 giây.

Sau 1 phút cả 2 máy bay bay được quãng đường dài \(1.v = v\)
Áp dụng công thức tính độ cao của máy bay so với mặt đất, ta tính được độ cao của hai máy bay 1 và 2 như sau:
Độ cao của máy bay 1: \({h_1} = v.\sin {10^0} \approx 0,17v\)
Độ cao của máy bay 2: \({h_2} = v.\sin {15^0} \approx 0,26v\)
Do đó, ta thấy rằng độ cao của máy bay 2 lớn hơn độ cao của máy bay 1. Vì vậy, máy bay 2 ở độ cao so với mặt đất lớn hơn sau 1 phút kể từ khi cất cánh.

tham khảo:
Thông tin trên không đủ để ta xác định độ cao của máy bay so với mặt đất phẳng, tại thời điểm 1 phút kể từ khi máy bay cất cánh mà chỉ tính được quãng đường bay của máy bay bay được.

a, Xét tam giác AHT vuông tại H, ta có:
\(cot\alpha=\dfrac{TH}{AH}\Rightarrow TH=AH\cdot cot\alpha=500\cdot cot\alpha\)
Vậy trên trục \(T_x\) tọa độ \(x_H=500\cdot cot\alpha\)
b, Ta có đồ thị của hàm số \(y=cot\alpha\) trong khoảng \(\dfrac{\pi}{6}< \alpha< \dfrac{2\pi}{3}\)
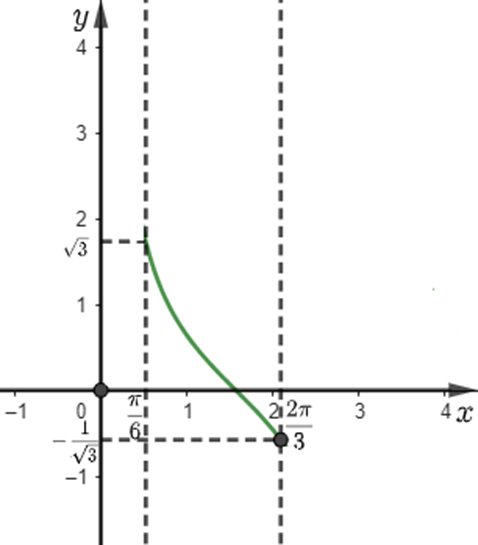
Khi đó:
\(-\dfrac{1}{\sqrt{3}}< cot\alpha< \dfrac{1}{\sqrt{3}}\Leftrightarrow-\dfrac{500}{\sqrt{3}}< 500\cdot cot\alpha< \dfrac{500}{\sqrt{3}}\\ \Leftrightarrow-\dfrac{500}{\sqrt{3}}< x_H< \dfrac{500}{\sqrt{3}}\\ \Leftrightarrow-288,7< x_H< 866\)
Vậy \(x\in\left\{-288,7;866\right\}\)

Đáp án : A
Nếu đi bằng ô tô có 15 cách.
Nếu đi bằng tàu hỏa có 5 cách.
Nếu đi bằng tàu thủy có 2 cách.
Nếu đi bằng máy bay có 2 cách.
Theo qui tắc cộng, ta có 15+5+2+2=24 cách chọn.

Nếu đi bằng ô tô có 10 cách.
Nếu đi bằng tàu hỏa có 5 cách.
Nếu đi bằng tàu thủy có 3 cách.
Nếu đi bằng máy bay có 2 cách.
Theo qui tắc cộng, ta có 10 + 5+ 3+ 2= 20 cách chọn.
Chọn đáp án A.

a, Ta có:
\(48=16+32\\ 80=48+32\\ 112=80+32\\ 144=112+32\\ ...\)
Vậy dãy số trên là cấp số cộng có số hạng đầu \(u_1=16\) và công sai \(d=32\)
b, Tổng chiều dài quãng đường rơi tự do của người đó trong 10s đầu tiên là:
\(S_{10}=\dfrac{10\cdot\left[u_1+\left(10-1\right)d\right]}{2}=\dfrac{10\cdot\left[2u_1+9d\right]}{2}=\dfrac{10\cdot\left(2\cdot16+9\cdot32\right)}{2}=1600\left(feet\right)\)